1. Integration by Parts

Recall:       \(\displaystyle \int u\,dv=u\,v-\int v\,du\)   where   \(du=\dfrac{du}{dx}\,dx\)   and   \(dv=\dfrac{dv}{dx}\,dx\)

Exercises

a. Indefinite Integrals

1

2

Use integration by parts to compute the following integrals:

1. \(\displaystyle \int xe^{2x}\,dx\)

   \(\displaystyle \int xe^{2x}\,dx =\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}+C\)

   For the parts take \[\begin{array}{ll} u=x & dv=e^{2x}\,dx \\ du=dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] Then \[\begin{aligned} \int xe^{2x}\,dx &=\dfrac{1}{2}xe^{2x}-\dfrac{1}{2}\int e^{2x}\,dx \\ &=\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}\), then \[ f'(x)=\dfrac{1}{2}e^{2x}+xe^{2x}-\dfrac{1}{2}e^{2x}=xe^{2x} \]

2. \(\displaystyle \int xe^{-3x}\,dx\)

   \(\displaystyle \int xe^{-3x}\,dx=-\,\dfrac{1}{3}xe^{-3x}-\dfrac{1}{9}e^{-3x}+C\)

   For the parts take \[\begin{array}{ll} u=x & dv=e^{-3x}\,dx \\ du=dx \quad & v=-\,\dfrac{1}{3}e^{-3x} \end{array}\] Then \[\begin{aligned} \int xe^{-3x}\,dx &=-\,\dfrac{1}{3}xe^{-3x}+\dfrac{1}{3}\int e^{-3x}\,dx \\ &=-\,\dfrac{1}{3}xe^{-3x}-\dfrac{1}{9}e^{-3x}+C \end{aligned}\]

   lk 

   Check by differentiating. If   \(f(x)=-\,\dfrac{1}{3}xe^{-3x}-\dfrac{1}{9}e^{-3x}\),   then \[ f'(x)=-\,\dfrac{1}{3}e^{-3x}+xe^{-3x}+\dfrac{1}{3}e^{-3x}=xe^{-3x} \]

3. \(\displaystyle \int xe^{-x}\,dx\)

   \(\displaystyle \int xe^{-x}\,dx=-xe^{-x}-e^{-x}+C\)

   For the parts take \[\begin{array}{ll} u=x & dv=e^{-x}\,dx \\ du=dx \quad & v=-e^{-x} \end{array}\] Then \[\begin{aligned} \int xe^{-x}\,dx &=-xe^{-x}+\int e^{-x}\,dx \\ &=-xe^{-x}-e^{-x}+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=-xe^{-x}-e^{-x}\), then \[ f'(x)=-e^{-x}+xe^{-x}+e^{-x}=xe^{-x} \]

4. \(\displaystyle \int (x-2)e^{x+1}\,dx\;\)

   \(\displaystyle \int (x-2)e^{x+1}\,dx=(x-3)e^{x+1}+C\)

   For the parts take \[\begin{array}{ll} u=x-2 & dv=e^{x+1}\,dx \\ du=dx \quad & v=e^{x+1} \end{array}\] Then \[\begin{aligned} \int (x-2)e^{x+1}\,dx &=(x-2)e^{x+1}-\int e^{x+1}\,dx \\ &=(x-2)e^{x+1}-e^{x+1}+C\\ &=xe^{x+1}-2e^{x+1}-e^{x+1}+C\\ &=xe^{x+1}-3e^{x+1}+C\\ &=(x-3)e^{x+1}+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=(x-3)e^{x+1}\), then \[\begin{aligned} f'(x) &=e^{x+1}+(x-3)e^{x+1} \\ &=e^{x+1}+xe^{x+1}-3e^{x+1} \\ &=xe^{x+1}-2e^{x+1} \\ &=(x-2)e^{x+1} \end{aligned}\]

5. \(\displaystyle \int \dfrac{2x}{e^x}\,dx\;\)

   \(\displaystyle \dfrac{1}{e^x}=e^{-x}\)

   \(\displaystyle \int \dfrac{2x}{e^x}\,dx=\dfrac{-2x-2}{e^x}+C\)

   Take the parts \[\begin{array}{ll} u=2x & dv=\dfrac{1}{e^x}\,dx=e^{-x}\,dx \\ du=2\,dx \quad & v=-e^{-x} \end{array}\] Then \[\begin{aligned} \int \dfrac{2x}{e^x}\,dx &=-2xe^{-x}+2\int e^{-x}\,dx \\ &=-2xe^{-x}-2e^{-x}+C \\ &=\dfrac{-2x-2}{e^x}+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=\dfrac{-2x-2}{e^x}=-2xe^{-x}-2e^{-x}\), then \[ f'(x)=-2e^{-x}+2xe^{-x}+2e^{-x}=\dfrac{2x}{e^x} \]

6. \(\displaystyle \int (1+x)e^{-3x}\,dx\;\)

   Use the parts \(u=x+1\) and \(dv=e^{-3x}\,dx\).

   \(\displaystyle \int (1+x)e^{-3x}\,dx =-\,\dfrac{4}{9}e^{-3x}-\dfrac{1}{3}xe^{-3x}+C\)

   Take the parts \[\begin{array}{ll} u=1+x & dv=e^{-3x}\,dx \\ du=dx \quad & v=\dfrac{-1}{3}e^{-3x} \end{array}\] Then \[\begin{aligned} \int (1+x)e^{-3x}\,dx &=-\,\dfrac{1}{3}\left(1+x\right)e^{-3x}+\dfrac{1}{3}\int e^{-3x}\,dx \\ &=-\,\dfrac{1}{3}e^{-3x}-\dfrac{1}{3}xe^{-3x}-\dfrac{1}{9}e^{-3x}+C \\ &=-\,\dfrac{4}{9}e^{-3x}-\dfrac{1}{3}xe^{-3x}+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=-\,\dfrac{4}{9}e^{-3x}-\dfrac{1}{3}xe^{-3x}\), then \[ f'(x)=\dfrac{4}{3}e^{-3x}-\dfrac{1}{3}e^{-3x}+xe^{-3x}=e^{-3x}+xe^{-3x}=(1+x)e^{-3x} \]

7. \(\displaystyle \int (x^2+1)\sin 2x\,dx\)

   Use the parts \(u=x^2+1\) and \(dv=\sin 2x\,dx\)

   \(\displaystyle\begin{aligned} \int &(x^2+1)\sin 2x\,dx \\ &=-\,\dfrac{1}{2}x^2\cos 2x+\dfrac{1}{2}x\sin 2x-\dfrac{1}{4}\cos 2x+C \end{aligned}\)

   We take the parts \[\begin{array}{ll} u=x^2+1 & dv=\sin 2x\,dx \\ du=2x\,dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\] Then \[\begin{aligned} \int (x^2+1)\sin 2x\,dx &=-\,\dfrac{1}{2}(x^2+1)\cos 2x+\int x\cos 2x\,dx \\ \end{aligned}\] We do another integration by parts using \[\begin{array}{ll} u=x & dv=\cos 2x\,dx \\ du=\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\] Thus \[\begin{aligned} \int (x^2+1)&\sin 2x\,dx \\ &=-\,\dfrac{1}{2}(x^2+1)\cos 2x+\left(\dfrac{1}{2}x\sin 2x-\dfrac{1}{2}\int \sin 2x\,dx\right) \\ &=-\,\dfrac{1}{2}x^{2}\cos 2x-\dfrac{1}{2}\cos 2x+\dfrac{1}{2}x\sin 2x+\dfrac{1}{4}\cos 2x+C \\ &=-\,\dfrac{1}{2}x^{2}\cos 2x+\dfrac{1}{2}x\sin 2x-\dfrac{1}{4}\cos 2x+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=-\,\dfrac{1}{2}x^2\cos 2x+\dfrac{1}{2}x\sin 2x-\dfrac{1}{4}\cos 2x\), then \[\begin{aligned} f'(x) &=-x\cos 2x+x^{2}\sin 2x+\dfrac{1}{2}\sin 2x+x\cos 2x+\dfrac{1}{2}\sin 2x \\ &=x^{2}\sin 2x+\sin 2x \\ &=(x^2+1)\sin 2x \end{aligned}\]

8. \(\displaystyle \int (x^2-4)\cos 3x\,dx\)

   Use the parts \(u=x^2-4\) and \(dv=\cos 3x\,dx\).

   \(\displaystyle\begin{aligned} \int &(x^2-4)\cos 3x\,dx \\ &=\dfrac{1}{3}x^2\sin 3x+\dfrac{2}{9}x\cos 3x-\dfrac{38}{27}\sin3x+C \end{aligned}\)

   We take the parts: \[\begin{array}{ll} u=x^2-4 & dv=\cos 3x\,dx \\ du=2x\,dx \quad & v=\dfrac{1}{3}\sin 3x \end{array}\] Then \[\begin{aligned} \int (x^2-4)\cos 3x\,dx &=\dfrac{1}{3}(x^2-4)\sin 3x-\dfrac{2}{3}\int x\sin 3x\,dx \\ \end{aligned}\] We do another integration by parts using: \[\begin{array}{ll} u=x & dv=\sin 3x\,dx \\ du=dx \quad & v=-\,\dfrac{1}{3}\cos 3x \end{array}\] Thus \[\begin{aligned} \int (x^2-4)&\cos 3x\,dx \\ &=\dfrac{1}{3}(x^2-4)\sin 3x-\dfrac{2}{3}\left(-\,\dfrac{1}{3}x\cos 3x+\dfrac{1}{3}\int \cos 3x\,dx\right) \\ &=\dfrac{1}{3}x^{2}\sin 3x-\dfrac{4}{3}\sin 3x+\dfrac{2}{9}x\cos 3x-\dfrac{2}{27}\sin 3x+C \\ &=\dfrac{1}{3}x^{2}\sin 3x+\dfrac{2}{9}x\cos 3x-\dfrac{38}{27}\sin 3x+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=\dfrac{1}{3}x^2\sin 3x+\dfrac{2}{9}x\cos 3x-\dfrac{38}{27}\sin 3x\), then \[\begin{aligned} f'(x) &=\dfrac{2}{3}x\sin 3x+x^{2}\cos 3x+\dfrac{2}{9}\cos 3x-\dfrac{2}{3}x\sin 3x-\dfrac{38}{9}\cos 3x \\ &=x^{2}\cos 3x-4\cos 3x \\ &=(x^2-4)\cos 3x \end{aligned}\]

9. \(\displaystyle \int x(x^3+1)\,dx\;\)

   Use the parts \(u=x\) and \(dv=(x^3+1)\,dx\).
   Or find a simpler method.

   \(\displaystyle \int x(x^3+1)\,dx=\dfrac{1}{5}x^{5}+\dfrac{1}{2}x^2+C\)

   This problem can be solved using the parts \(u=x\) and \(dv=(x^3+1)\,dx\). However, it is easier to just expand the polynomial and integrate it:
   \[\begin{aligned} \int x(x^3+1)\,dx &=\int (x^4+x)\,dx \\ &=\dfrac{1}{5}x^{5}+\dfrac{1}{2}x^2+C \end{aligned}\]

   lk 

   Check by differentiating. If \(f(x)=\dfrac{1}{5}x^{5}+\dfrac{1}{2}x^{2}\), then \[ f'(x)=x^{4}+x=x(x^3+1) \]

10. \(\displaystyle \int x\sqrt{x-1}\,dx\)   Compute once by parts and once by substitution.

    Here are three equivalent answers:
    \(\begin{aligned} \int x\sqrt{x-1}\,dx &=\dfrac{2}{3}x(x-1)^{3/2}-\dfrac{4}{15}(x-1)^{5/2}+C \\ &=\dfrac{2}{5}(x-1)^{5/2}+\dfrac{2}{3}(x-1)^{3/2}+C \\ &=\left(\dfrac{2}{5}x+\dfrac{4}{15}\right)(x-1)^{3/2}+C \end{aligned}\)

    This integral can be computed using Integration by Parts with the parts: \[\begin{array}{ll} u=x & dv=\sqrt{x-1}\,dx \\ du=dx \quad & v=\dfrac{2}{3}(x-1)^{3/2} \end{array}\] Then, \[\begin{aligned} \int x\sqrt{x-1}\,dx &=x\left(\dfrac{2}{3}(x-1)^{3/2}\right) -\int \dfrac{2}{3}(x-1)^{3/2}\,dx \\ &=\dfrac{2}{3}x(x-1)^{3/2}-\dfrac{2}{3}\left(\dfrac{2}{5}(x-1)^{5/2}\right)+C \\ &=\dfrac{2}{3}x(x-1)^{3/2}-\dfrac{4}{15}(x-1)^{5/2}+C \end{aligned}\]

    lk 

    Although we solved this example using integration by parts, it is more efficient to solve it by using the method of substitution. We take \(u=x-1\). Then \(du=dx\) and \(x=u+1\). So: \[\begin{aligned} \int x\sqrt{x-1}\,dx &=\int (u+1)\sqrt{u}\,du =\int \left(u^{3/2}+u^{1/2}\right)\,du \\ &=\dfrac{2}{5}u^{5/2}+\dfrac{2}{3}u^{3/2}+C \\ &=\dfrac{2}{5}(x-1)^{5/2}+\dfrac{2}{3}(x-1)^{3/2}+C \end{aligned}\]

    lk 

    We check by differentiating (using the Product and Power Rules). \[\begin{aligned} \dfrac{d}{dx}&\left(\dfrac{2}{3}x(x-1)^{3/2}-\dfrac{4}{15}(x-1)^{5/2}\right) \\ &=\dfrac{2}{3}(x-1)^{3/2}+x(x-1)^{1/2}-\dfrac{4}{15}\dfrac{5}{2}(x-1)^{3/2} \\ &=x\sqrt{x-1} \end{aligned}\]

    We check by differentiating (using the Power Rule). \[\begin{aligned} \dfrac{d}{dx}&\left(\dfrac{2}{5}(x-1)^{5/2}+\dfrac{2}{3}(x-1)^{3/2}\right) \\ &=(x-1)^{3/2}+(x-1)^{1/2} \\ &=((x-1)+1)\sqrt{x-1} \\ &=x\sqrt{x-1} \end{aligned}\]

    Which of the two ways to compute this integral is better? The substitution is quicker but both are OK.

    
    The first answer simplifies to \[\begin{aligned} \dfrac{2}{3}x(x-1)^{3/2}-\dfrac{4}{15}(x-1)^{5/2} &=\left[\dfrac{2}{3}x-\dfrac{4}{15}(x-1)\right](x-1)^{3/2} \\ &=\left(\dfrac{2}{5}x+\dfrac{4}{15}\right)(x-1)^{3/2} \end{aligned}\] The second answer simplifies to \[\begin{aligned} \dfrac{2}{5}(x-1)^{5/2}+\dfrac{2}{3}(x-1)^{3/2} &=\left[\dfrac{2}{5}(x-1)+\dfrac{2}{3}\right](x-1)^{3/2} \\ &=\left(\dfrac{2}{5}x+\dfrac{4}{15}\right)(x-1)^{3/2} \end{aligned}\] They're equal!

11. \(\displaystyle \int x\csc^2 2x\,dx\)

    \(\displaystyle \int x\csc^2 2x\,dx =-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{4}\ln|\sin 2x|+C\)

    We use the parts \[\begin{array}{ll} u=x & dv=\csc^2 2x \\ du=dx \quad & v=-\,\dfrac{1}{2}\cot 2x \end{array}\] This gives \[\begin{aligned} \int x\csc^2 2x\,dx &=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{2}\int \cot 2x\,dx \\ &=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{2}\int \dfrac{\cos 2x}{\sin 2x}\,dx \end{aligned}\] We now use the substitution \(u=\sin 2x\), with \(du=2\cos 2x\,dx\), to get \[\begin{aligned} \int x\csc^2 2x\,dx &=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{4}\int \dfrac{1}{u}\,du \\ &=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{4}\ln|u|+C \\ &=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{4}\ln|\sin 2x|+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=-\,\dfrac{1}{2}x\cot 2x+\dfrac{1}{4}\ln|\sin 2x|\),   then \[ f'(x)=-\,\dfrac{1}{2}\cot 2x+x\csc^2 2x+\dfrac{1}{2}\dfrac{\cos 2x}{\sin 2x} =x\csc^2 2x \]

12. \(\displaystyle \int (x+1)\sin(x+1)\,dx\)

    \(\displaystyle \int (x+1)\sin(x+1)\,dx =-(x+1)\cos(x+1)+\sin(x+1)+C\)

    Don't expand the function in the problem for example by writing \(\sin(x+1)=\sin x\cos 1+\cos x\sin 1\). This unnecessarily complicates the solution.
    We use the parts: \[\begin{array}{ll} u=x+1 & dv=\sin(x+1)\,dx \\ du=dx \quad & v=-\cos(x+1) \end{array}\] Then \[\begin{aligned} \int (x+1)\sin(x+1)\,dx &=-(x+1)\cos(x+1)+\int \cos(x+1)\,dx \\ &=-(x+1)\cos(x+1)+\sin(x+1)+C \end{aligned}\] Alternatively, first make the substitution \(\theta=x+1\).

    lk 

    We check by differentiating. If   \(f(x)=-(x+1)\cos(x+1)+\sin(x+1)\),   then \[\begin{aligned} f'(x) &=-\cos(x+1)+(x+1)\sin(x+1)+\cos(x+1) \\ &=(x+1)\sin(x+1) \end{aligned}\]

13. \(\displaystyle \int (x+2)\cos(x+1)\,dx\)

    \(\displaystyle \int (x+2)\cos(x+1)\,dx=(x+2)\sin(x+1)+\cos(x+1)+C\)

    We use the parts: \[\begin{array}{ll} u=x+2 & dv=\cos(x+1)\,dx \\ du=dx \quad & v=\sin(x+1) \end{array}\] Then \[\begin{aligned} \int (x+2)\cos(x+1)\,dx &=(x+2)\sin(x+1)-\int \sin(x+1)\,dx \\ &=(x+2)\sin(x+1)+\cos(x+1)+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=(x+2)\sin(x+1)+\cos(x+1)\),   then \[\begin{aligned} f'(x) &=\sin(x+1)+(x+2)\cos(x+1)-\sin(x+1) \\ &=(x+1)\cos(x+1) \end{aligned}\]

14. \(\displaystyle \int x(e^x+2)(e^x-2)\,dx\)

    First multiply out the integrand and split the integral in two: \[\begin{aligned} \int x(e^x+2)(e^x-2)\,dx &=\int x(e^{2x}-4)\,dx \\ &=\int xe^{2x}\,dx-4\int x\,dx \end{aligned}\]

    \(\displaystyle \int x(e^x+2)(e^x-2)\,dx =\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}-2x^2+C\)

    We first multiply out the integrand and split the integral in two: \[\begin{aligned} \int x(e^x+2)(e^x-2)\,dx &=\int x(e^{2x}-4)\,dx \\ &=\int xe^{2x}\,dx-4\int x\,dx \end{aligned}\] For the first integral we use the parts: \[\begin{array}{ll} u=x & dv=e^{2x}\,dx \\ du=dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] Then \[\begin{aligned} \int x(e^x+2)(e^x-2)\,dx &=\dfrac{1}{2}xe^{2x}-\dfrac{1}{2}\int e^{2x}\,dx-4\int x\,dx \\ &=\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}-2x^2+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=\dfrac{1}{2}xe^{2x}-\dfrac{1}{4}e^{2x}-2x^2\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}e^{2x}+xe^{2x}-\dfrac{1}{2}e^{2x}-4x \\ &=xe^{2x}-4x=x(e^{2x}-4) \\ &=x(e^x+2)(e^x-2) \end{aligned}\]

15. \(\displaystyle \int p^2e^{-p}\,dp\)

    \(\displaystyle \int p^2e^{-p}\,dp =-p^2e^{-p}-2pe^{-p}-2e^{-p}+C\)

    We use the parts \[\begin{array}{ll} u=p^2 & dv=e^{-p}dp \\ du=2p\,dp \quad & v=-e^{-p} \end{array}\] This gives \[\begin{aligned} \int p^2e^{-p}\,dx &=-p^2e^{-p}+2\int pe^{-p}\,dp \end{aligned}\] We need to use parts again. \[\begin{array}{ll} u=p & dv=e^{-p}dp \\ du=\,dp \quad & v=-e^{-p} \end{array}\] Then: \[\begin{aligned} \int p^2e^{-p}\,dp &=-p^2e^{-p}+2(-pe^{-p}+\int e^{-p}\,dp) \\ &=-p^2e^{-p}+2(-pe^{-p}-e^{-p})+C \\ &=-p^2e^{-p}-2pe^{-p}-2e^{-p}+C \end{aligned}\]

    lk 

    We differentiate   \(f(x)=-p^2e^{-p}-2pe^{-p}-2e^{-p}\): \[\begin{aligned} f'(x) &=-2pe^{-p}+p^2e^{-p}-2e^{-p}+2pe^{-p}+2e^{-p} \\ &=p^2e^{-p} \end{aligned}\]

16. \(\displaystyle \int p^3e^{p^2}\,dp\)

    Selecting the parts for this one is more subtle.
    Take the parts to be \(u=p^2\) and \(dv=pe^{p^2}\,dp\) so that is easier to find \(v\).
    Alternatively, first make the substitution \(w=p^2\).

    \(\displaystyle \int p^3e^{p^2}\,dp =\dfrac{1}{2}p^2e^{p^2}-\dfrac{1}{2}e^{p^2 }+C\)

    The parts are tricky because we need to be able to find the antiderivative of \(dv\). Since \(\dfrac{d}{dp}e^{p^2}=2pe^{p^2}\), we use the parts: \[\begin{array}{ll} u=p^2 & dv=pe^{p^2}\,dp \\ du=2p\,dp \quad & v=\dfrac{1}{2}e^{p^2} \end{array}\] This gives \[\begin{aligned} \int p^3e^{p^2}\,dp &=\int p^2\cdot pe^{p^2}\,dp \\ &=\dfrac{1}{2}p^2e^{p^2}-\int pe^{p^2}\,dp \\ &=\dfrac {1}{2}p^2e^{p^2}-\dfrac{1}{2}e^{p^2}+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=\dfrac{1}{2}p^2e^{p^2}-\dfrac{1}{2}e^{p^2}\),   then \[\begin{aligned} f'(x) &=pe^{p^2}+\dfrac{1}{2}p^22pe^{p^2}-pe^{p^2} \\ &=p^3e^{p^2} \end{aligned}\]

    Alternatively, we can first substitue \(w=p^2\) with \(dw=2p\,dp\): \[ \int p^3e^{p^2}\,dp=\dfrac{1}{2}\int we^{w}\,dw \] We now take the parts: \[\begin{array}{ll} u=w & dv=e^{w}dw \\ du= dw \quad & v=e^{w} \end{array}\] \[\begin{aligned} \int p^3e^{p^2}\,dp &=\dfrac{1}{2}(we^{w}-\int e^{w}dw) \\ &=\dfrac{1}{2}we^{w}-\dfrac{1}{2}e^{w}+C \\ \end{aligned}\] We substitute back \(w=p^2\): \[ \int p^3e^{p^2}\,dp =\dfrac{1}{2}p^2e^{p^2}-\dfrac{1}{2}e^{p^2}+C \] Which method was easier?

17. \(\displaystyle \int (x^2+x-1)e^{3x}\,dx\)

    \(\displaystyle \int (x^2+x-1)e^{3x}\,dx =\left(\dfrac{1}{3}x^2+\dfrac{1}{9}x-\dfrac{10}{27}\right)e^{3x}+C\)

    We use the parts \[\begin{array}{ll} u=x^2+x-1 & dv=e^{3x}\,dx \\ du=(2x+1)\,dx \quad & v=\dfrac{1}{3}e^{3x} \end{array}\] Then \[\begin{aligned} \int &(x^2+x-1)e^{3x}\,dx \\ &=\dfrac{1}{3}(x^2+x-1)e^{3x}-\dfrac{1}{3}\int (2x+1)e^{3x}dx \\ \end{aligned}\] We need to take parts again: \[\begin{array}{ll} u=2x+1 & dv=e^{3x}dx \\ du=2dx \quad & v=\dfrac{1}{3}e^{3x} \end{array}\] Thus \[\begin{aligned} \int &(x^2+x-1)e^{3x}\,dx \\ &=\dfrac{1}{3}(x^2+x-1)e^{3x} -\dfrac{1}{3}\left(\dfrac{1}{3}e^{3x}(2x+1)-\dfrac{2}{3}\int e^{3x}\,dx\right) \\ &=\dfrac{1}{3}(x^2+x-1)e^{3x}-\dfrac{1}{9}e^{3x}(2x+1)+\dfrac{2}{27}e^{3x}+C \\ &=\left(\dfrac{1}{3}x^2+\dfrac{1}{3}x-\dfrac{1}{3}-\dfrac{2}{9}x -\dfrac{1}{9}+\dfrac{2}{27}\right)e^{3x}+C \\ &=\left(\dfrac{1}{3}x^2+\dfrac{1}{9}x-\dfrac{10}{27}\right)e^{3x}+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=\dfrac{1}{3}x^2e^{3x}+\dfrac{1}{9}xe^{3x}-\dfrac{10}{27}e^{3x}\),   then \[\begin{aligned} f'(x) &=\dfrac{2}{3}xe^{3x}+x^2e^{3x}+\dfrac{1}{9}e^{3x}+\dfrac{1}{3}xe^{3x}-\dfrac{10}{9}e^{3x} \\ &=x^2e^{3x}+xe^{3x}-e^{3x} \\ &=(x^2+x-1)e^{3x} \end{aligned}\]

18. \(\displaystyle \int (x^2-x+1)e^{ax}\,dx\;\)

    Take the parts \(u=x^2-x+1\) and \(dv=e^{ax}\,dx\).
    You will need two integrations by parts to complete the computation.

    \(\displaystyle\begin{aligned} \int &(x^2-x+1)e^{ax}\,dx \\ &=\left(\dfrac{x^2-x+1}{a}-\dfrac{2x-1}{a^2 } +\dfrac{2}{a^3 }\right)e^{ax}+C \end{aligned}\)

    We use the parts \[\begin{array}{ll} u=x^2-x+1 & dv=e^{ax}\,dx \\ du=(2x-1)\,dx \quad & v=\dfrac{1}{a}e^{ax} \end{array}\] Then \[\begin{aligned} \int &(x^2-x+1)e^{ax}\,dx \\ &=\dfrac{1}{a}(x^2-x+1)e^{ax}-\dfrac{1}{a}\int (2x-1)e^{ax}\,dx \end{aligned}\] This time we take the parts: \[\begin{array}{ll} u=2x-1 & dv=e^{ax}\,dx \\ du=2\,dx \quad & v=\dfrac{1}{a}e^{ax} \end{array}\] Thus \[\begin{aligned} \int &(x^2+x-1)e^{3x}\,dx \\ &=\dfrac{x^2-x+1}{a}e^{ax} -\dfrac{1}{a}\left(\dfrac{2x-1}{a}e^{ax}-\dfrac{2}{a}\int e^{ax}\,dx\right) \\ &=\dfrac{x^2-x+1}{a}e^{ax}-\dfrac{2x-1}{a^2}e^{ax}+\dfrac{2}{a^3}e^{ax}+C \\ &=\left(\dfrac{x^2-x+1}{a}-\dfrac{2x-1}{a^2}+\dfrac{2}{a^3}\right)e^{ax}+C \end{aligned}\]

    lk 

    We check by differentiating. If \[ f(x)=\left(\dfrac{x^2-x+1}{a}-\dfrac{2x-1}{a^2 } +\dfrac{2}{a^3 }\right)e^{ax} \] then \[\begin{aligned} f'(x) &=\left(\dfrac{2x-1}{a}-\dfrac{2}{a^2}\right)e^{ax} +\left(\dfrac{x^2-x+1}{a}-\dfrac{2x-1}{a^2 } +\dfrac{2}{a^3 }\right)ae^{ax} \\ &=\left(\dfrac{2x-1}{a}-\dfrac{2}{a^2}\right)e^{ax} +\left(x^2-x+1-\dfrac{2x-1}{a} +\dfrac{2}{a^2}\right)e^{ax} \\ &=(x^2-x+1)e^{ax} \end{aligned}\]

19. \(\displaystyle \int (x-1)^2e^{-x}\,dx\)

    \(\displaystyle \int (x-1)^2e^{-x}\,dx=-(x^2+1)e^{-x}+C\)

    We use the parts \[\begin{array}{ll} u=(x-1)^2 & dv=e^{-x}\,dx \\ du=2(x-1)\,dx \quad & v=-e^{-x} \end{array}\] Then \[\begin{aligned} \int (x-1)^2e^{-x}\,dx &=-(x-1)^2e^{-x}+2\int (x-1)e^{-x}\,dx \end{aligned}\] We now take the parts: \[\begin{array}{ll} u=(x-1) & dv=e^{-x}\,dx \\ du=dx \quad & v=-e^{-x} \end{array}\] Thus \[\begin{aligned} \int &(x-1)^2e^{-x}\,dx \\ &=-(x-1)^2e^{-x}+2\left(-(x-1)e^{-x}+\int e^{-x}\,dx\right) \\ &=-(x-1)^2e^{-x}+2\left(-(x-1)e^{-x}-e^{-x}\right)+C \\ &=-(x^2-2x+1)e^{-x}-(2x-2)e^{-x}-2e^{-x}+C \\ &=(-x^2+2x-1-2x+2-2)e^{-x}+C \\ &=-(x^2+1)e^{-x}+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=-(x^2+1)e^{-x}\),   then \[\begin{aligned} f'(x) &=-(2x)e^{-x}+(x^2+1)e^{-x} \\ &=(x^2-2x+1)e^{-x} \\ &=(x-1)^2e^{-x} \end{aligned}\] which is what we started with.

20. \(\displaystyle \int (x-1)\cos x\,dx\)

    \(\displaystyle \int (x-1)\cos x\,dx =(x-1)\sin x+\cos x +C\)

    We use the parts \[\begin{array}{ll} u=(x-1) & dv=\cos x\,dx \\ du= dx \quad & v=\sin x \end{array}\] Then \[\begin{aligned} \int (x-1)\cos x\,dx &=(x-1)\sin x-\int \sin x\,dx \\ &=(x-1)\sin x+\cos x+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=(x-1)\sin x+\cos x\),   then \[\begin{aligned} f'(x) &=\sin x+(x-1)\cos x-\sin x \\ &=(x-1)\cos x \end{aligned}\]

21. \(\displaystyle \int x^2\sin x\,dx\)

    \(\displaystyle \int x^2\sin x\,dx=-x^2\cos x+2x\sin x+2\cos x+C\)

    First let:   \[\begin{array}{ll} u=x^2 & dv=\sin x\,dx \\ du=2x\,dx \quad & v=-\cos x \end{array}\]
    So: \[ \int x^2\sin x\,dx=-x^2\cos x+\int 2x\cos x \] Now let:   \[\begin{array}{ll} u=2x & dv=\cos x\,dx \\ du=2\,dx \quad & v=\sin x \end{array}\]
    So: \[\begin{aligned} \int x^2\sin x\,dx &=-x^2\cos x+2x\sin x-\int 2\sin x\,dx \\ &=-x^2\cos x+2x\sin x+2\cos x+C \end{aligned}\]

    lk 

    We check by differentiating. If   \(f(x)=-x^2\cos x+2x\sin x+2\cos x\),   then \[\begin{aligned} f'(x) &=-2x\cos x+x^2\sin x+2\sin x+2x\cos x-2\sin x \\ &=x^2\sin x \end{aligned}\]

b. Choosing the 'Parts'

1

2

Use integration by parts to compute the following integrals:

22. \(\displaystyle \int \dfrac{\ln|x|}{x^2}\,dx\;\)

    Take \(u=\ln|x|\) and \(dv=\dfrac{1}{x^2}\,dx\).

    \(\displaystyle \int \dfrac{\ln|x|}{x^2}\,dx =-\,\dfrac{\ln|x|}{x}-\dfrac{1}{x}+C\)

    This is a product of a log function and a power function. So LAPTE tells us that \(u\) should be the log function. So we take the parts: \[\begin{array}{ll} u=\ln|x| & dv=\dfrac{1}{x^2}\,dx \\[7pt] du=\dfrac{1}{x}\,dx \quad & v=-\,\dfrac{1}{x} \end{array}\] Hence \[\begin{aligned} \int \dfrac{\ln|x|}{x^2}\,dx =-\,\dfrac{\ln|x|}{x}+\int \dfrac{1}{x^2}\,dx \\ =-\,\dfrac{\ln|x|}{x}-\dfrac{1}{x}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{1}{x}\ln|x|-\dfrac{1}{x}\),   then \[ f'(x)=\dfrac{1}{x^2}\ln|x|-\dfrac{1}{x^2}+\dfrac{1}{x^2} =\dfrac{\ln|x|}{x^2} \]

23. \(\displaystyle \int s^2\ln s\,ds\)

    Take the parts \(u=\ln s\) and \(dv=s^2\,ds\).

    \(\displaystyle \int s^2\ln s\,ds =\dfrac{s^3\ln s}{3}-\dfrac{s^3}{9}+C\)

    We take \[\begin{array}{ll} u=\ln s & dv=s^2\,ds \\ du=\dfrac{1}{s}\,ds \quad & v=\dfrac{s^3}{3} \end{array}\] Hence \[\begin{aligned} \int s^2\ln s\,ds &=\dfrac{s^3\ln s}{3}-\dfrac{1}{3}\int s^2\,dx \\ &=\dfrac{s^3\ln s}{3}-\dfrac{s^3}{9}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{s^3}{3}\ln|s|-\dfrac{s^3}{9}\),   then \[ f'(x)=s^2\ln|s|+\dfrac{s^2}{3}-\dfrac{s^2}{3} =s^2\ln|s| \]

24. \(\displaystyle \int x\ln|x+1|\,dx\)

    \(\displaystyle \int x\ln|x+1|\,dx =\dfrac{(x^2-1)\ln|x+1|}{2}-\dfrac{x^2}{4}+\dfrac{x}{2}+C\)

    We integrate by parts with \[\begin{array}{ll} u=\ln|x+1| & dv=x\,dx \\ du=\dfrac{1}{x+1}\,dx \quad & v=\dfrac{x^2}{2} \end{array}\] So \[ \int x\ln|x+1|\,dx =\dfrac{x^2\ln|x+1|}{2}-\dfrac{1}{2}\int \dfrac{x^2}{x+1}\,dx \] By long division of polynomials, we have \[ \dfrac{x^2}{x+1}=x-1+\dfrac{1}{x+1} \] So: \[\begin{aligned} \int x\ln|x+1|\,dx &=\dfrac{x^2\ln|x+1|}{2}-\dfrac{1}{2}\int x-1+\dfrac{1}{x+1}\,dx \\ &=\dfrac{x^2\ln|x+1|}{2}-\dfrac{1}{2}\left(\dfrac{x^2}{2}-x+\ln|x+1|\right)+C \\ &=\dfrac{(x^2-1)\ln|x+1|}{2}-\dfrac{x^2}{4}+\dfrac{x}{2}+C \\ \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{x^2-1}{2}\ln|x+1|-\dfrac{x^2}{4}+\dfrac{x}{2}\),   then \[ f'(x)=x\ln|x+1|+\dfrac{x^2-1}{2}\dfrac{1}{x+1}-\dfrac{x}{2}+\dfrac{1}{2} =x\ln|x+1| \]

25. \(\displaystyle \int 3x\ln(x^2)\,dx\)

    Remember \(\ln(x^2)=2\ln|x|\). Then use the parts \(u=\ln|x|\) and \(dv=6x\,dx\).

    \(\displaystyle \int 3x\ln(x^2)\,dx =3x^2\ln|x|-\dfrac{3x^2}{2}+C\)

    We first rewrite the integrand using a log identity: \[ \int 3x\ln(x^2)\,dx=\int 6x\ln|x|\,dx \] We integrate by parts with \[\begin{array}{ll} u=\ln|x| & dv=6x\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=3x^2 \end{array}\] So \[\begin{aligned} \int 3x\ln(x^2)\,dx &=3x^2\ln|x|-3\int x\,dx \\ &=3x^2\ln|x|-\dfrac{3x^2}{2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=3x^2\ln|x|-\dfrac{3x^2}{2}\),   then \[ f'(x)=6x\ln|x|+3x-3x =3x\ln(x^2) \]

26. \(\displaystyle \int (\ln x)^2\,dx\)

    Let \(u=(\ln x)^2\) and \(dv=dx\).

    \(\displaystyle \int (\ln x)^2\,dx =x(\ln x)^2-2x\ln x+2x+C\)

    Let \[\begin{array}{ll} u=(\ln x)^2 & dv=dx \\ du=\dfrac{2(\ln x)}{x}\,dx \quad & v=x \end{array}\] So \[\begin{aligned} \int (\ln x)^2\,dx &=x(\ln x)^2-\int \dfrac{2x(\ln x)}{x}\,dx \\ &=x(\ln x)^2-2\int \ln x\,dx \\ &=x(\ln x)^2-2(x\ln x-x)+C \\ &=x(\ln x)^2-2x\ln x+2x+C \end{aligned}\] You should remenber \(\displaystyle \int \ln x\,dx=x\ln x-x+C\) which was derived in a previous exercise. Alternatively, we could do another integration by parts.

    lk 

    We check using the Product Rule. If   \(f(x)=x(\ln x)^2-2x\ln x+2x\),   then \[\begin{aligned} f'(x) &=(\ln x)^2+x2(\ln x)\dfrac{1}{x}-2\ln x-2x\dfrac{1}{x}+2 \\ &=(\ln x)^2+2(\ln x)-2\ln x-2+2 =(\ln x)^2 \end{aligned}\]

27. \(\displaystyle \int \ln(x^2)\,dx\)

    Use the log identity \(\ln(x^2)=2\ln|x|\).

    \(\displaystyle \int \ln(x^2)\,dx =2x\ln|x|-2x+C\)

    This is a trick problem. Simply use the log identity \(\ln(x^2)=2\ln|x|\). So: \[ \int \ln(x^2)\,dx=2\int \ln|x|\,dx=2(x\ln|x|-x)+C=2x\ln|x|-2x+C \] assuming you remember \(\displaystyle \int \ln|x|\,dx=x\ln x-x+C\) which was derived in a previous exercise.

    lk 

    We check using the Product Rule. If   \(f(x)=2x\ln|x|-2x\),   then \[ f'(x)=2\ln|x|+2-2 =2\ln|x| =\ln(x^2) \]

28. \(\displaystyle \int \arcsin 2x\,dx\)

    \(\displaystyle \int \arcsin 2x\,dx =x\arcsin 2x+\dfrac{\sqrt{1-4x^2}}{2}+C\)

    Take \[\begin{array}{ll} u=\arcsin 2x & dv=\,dx \\ du=\dfrac{2}{\sqrt{1-4x^2}}\,dx \quad & v=x \end{array}\] Thus \[ \int \arcsin 2x\,dx =x\arcsin 2x-2\int \dfrac{x}{\sqrt{1-4x^2}}\,dx \] To compute the remaining integral, use the substitution \(z=1-4x^2\). Then \(dz=-8x\,dx\) and \(x\,dx=-\,\dfrac{1}{8}\,dz\). Thus, \[\begin{aligned} \int \arcsin 2x\,dx &=x\arcsin 2x+\dfrac{1}{4}\int \dfrac{1}{\sqrt{z}}\,dz \\ &=x\arcsin 2x+\dfrac{1}{2}\sqrt{z}+C \\ &=x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}+C \\ \end{aligned}\]

    If you remember from a previous example: (You're not expected to remember this one.) \[ \int \arcsin u\,du=u\arcsin u+\sqrt{1-u^2}+C \] then the substitution \(u=2x\) will also work.

    lk 

    We check using the Product Rule. If   \(f(x)=x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}\),   then \[\begin{aligned} f'(x) &=\arcsin 2x+\dfrac{2x}{\sqrt{1-4x^2}}+\dfrac{1}{4}\dfrac{-8x}{\sqrt{1-4x^2}} \\ &=\arcsin 2x+\dfrac{2x}{\sqrt{1-4x^2}}-\dfrac{2x}{\sqrt{1-4x^2}} \\ &=\arcsin 2x \end{aligned}\]

29. \(\displaystyle \int \arctan 3x\,dx\)

    \(\displaystyle \int \arctan 3x\,dx =x\arctan 3x-\dfrac{1}{6}\ln(1+9x^2)+C\)

    Take \[\begin{array}{ll} u=\arctan 3x & dv=dx \\ du=\dfrac{3}{1+9x^2}\,dx \quad & v=x \end{array}\] Thus \[ \int \arctan 3x\,dx=x\arctan 3x-\int \dfrac{3x}{1+9x^2}\,dx \] To compute the second integral, use the substitution \(z=1+9x^2\). Then \(dz=18x\,dx\) and \(3x\,dx=\dfrac{1}{6}\,dz\). Thus: \[\begin{aligned} \int \arctan 3x\,dx &=x\arctan 3x-\dfrac{1}{6}\int \dfrac{1}{z}\,dz \\ &=x\arctan 3x-\dfrac{1}{6}\ln|z|+C \\ &=x\arctan 3x-\dfrac{1}{6}\ln(1+9x^2)+C \end{aligned}\]

    You may remember from a previous exercise: (You're not expected to remember this one.) \[ \int \arctan u\,du =u\arctan u-\dfrac{1}{2}\ln(1+u^2)+C \] Then the substitution \(u=3x\) will also work.

    lk 

    We check using the Product Rule. If   \(f(x)=x\arctan 3x-\dfrac{1}{6}\ln(1+9x^2)\),   then \[\begin{aligned} f'(x) &=\arctan 3x+\dfrac{3x}{1+9x^2}-\dfrac{1}{6}\dfrac{18x}{1+9x^2} \\ &=\arctan 3x+\dfrac{3x}{1+9x^2}-\dfrac{3x}{1+9x^2} \\ &=\arctan 3x \end{aligned}\]

30. \(\displaystyle \int \arccos x\,dx\)

    Use integration by parts with \(u=\arccos x\) and \(dv=dx\).

    \(\displaystyle \int \arccos x\,dx =x\arccos x-\sqrt{1-x^2}+C\)

    We take: \[\begin{array}{ll} u=\arccos x & dv=dx \\ du=\dfrac{-1}{\sqrt{1-x^2}}\,dx \quad & v=x \end{array}\] Thus \[ \int \arccos x\,dx=x\arccos x+\int \dfrac{x}{\sqrt{1-x^2}}\,dx \] To compute the remaining integral, we use the substitution \(z=1-x^2\). Then \(dz=-2x\,dx\) and \(x\,dx=-\,\dfrac{1}{2}\,dz\). Thus: \[\begin{aligned} \int \arccos x\,dx &=x\arccos x-\dfrac{1}{2}\int \dfrac{1}{\sqrt{z}}\,dz \\ &=x\arccos x-\sqrt{z}+C \\ &=x\arccos x-\sqrt{1-x^2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\arccos x-\sqrt{1-x^2}\),   then \[ f'(x)=\arccos x+\dfrac{-x}{\sqrt{1-x^2}}+\dfrac{x}{\sqrt{1-x^2}} =\arccos x \]

31. \(\displaystyle \int \arccos(ax)\,dx\)

    Just use the substitution \(u=ax\) and then the previous problem.

    \(\displaystyle \int \arccos(ax)\,dx =x\arccos(ax)-\dfrac{\sqrt{1-a^2x^2}}{a}+C\)

    From the previous problem we know: \[ \int \arccos u\,du=u\arccos u-\sqrt{1-u^2}+C \] For this problem we make the substitution \(u=ax\): \[\begin{aligned} \int \arccos (ax)\,dx &=\dfrac{1}{a}\int \arccos (u)\,du \\ &=\dfrac{1}{a}\left[u\arccos u-\sqrt{1-u^2}\right]+C \\ &=\dfrac{1}{a}\left[ax\arccos ax-\sqrt{1-a^2x^2}\right]+C \\ &=x\arccos (ax)-\dfrac{\sqrt{1-a^2x^2}}{a}+C \end{aligned}\]

    lk 

    If   \(f(x)=x\arccos (ax)-\dfrac{\sqrt{1-a^2x^2}}{a} \),   then \[\begin{aligned} f'(x) &=\arccos (ax)-\dfrac{ax}{\sqrt{1-a^2x^2}}+\dfrac{2a^2x}{2a\sqrt{1-a^2x^2}} \\ &=\arccos (ax) \end{aligned}\]

32. \(\displaystyle \int \mathrm{arccot}\,x\,dx\)

    Use integration by parts with \(u=\mathrm{arccot}\,x\) and \(dv=dx\).

    \(\displaystyle \int \text{arccot}\,x\,dx =x\,\text{arccot}\,x+\dfrac{1}{2}\ln(1+x^2)+C\)

    We take: \[\begin{array}{ll} u=\mathrm{arccot}\,x & dv=dx \\ du=\dfrac{-1}{1+x^2}\,dx \quad & v=x \end{array}\] Thus \[ \int \mathrm{arccot}\,x\,dx=x\,\mathrm{arccot}\,x+\int \dfrac{x}{1+x^2}\,dx \] To compute the remaining integral, we use the substitution \(z=1+x^2\). Then \(dz=2x\,dx\) and \(x\,dx=\dfrac{1}{2}\,dz\). Thus: \[\begin{aligned} \int \mathrm{arccot}\,x\,dx &=x\,\mathrm{arccot}\,x+\dfrac{1}{2}\int \dfrac{1}{z}\,dz \\ &=x\,\mathrm{arccot}\,x+\dfrac{1}{2}\ln|z|+C \\ &=x\,\mathrm{arccot}\,x+\dfrac{1}{2}\ln(1+x^2)+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\,\mathrm{arccot}\,x+\dfrac{1}{2}\ln(1+x^2)\),   then \[ f'(x)=\mathrm{arccot}\,x+\dfrac{-x}{1+x^2}+\dfrac{x}{1+x^2} =\mathrm{arccot}\,x \]

---

33. An important function in statistics is the error function defined by \[ \mathrm{erf}(x)=\dfrac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt \] There is no exact formula for the result of this integral; it must be computed numerically. However, its derivative is easily found by the fundamental theorem of calculus: \[ \dfrac{d}{dx}(\mathrm{erf}(x)) =\dfrac{2}{\sqrt{\pi}}e^{-x^2} \] In addition, its antiderivative is easily found by integration by parts.
    Compute \(\displaystyle \int \mathrm{erf}(x)\,dx\).

    Use integration by parts with \(u=\text{erf}(x)\) and \(dv=dx\).

    \(\displaystyle \int \mathrm{erf}(x)\,dx =x\,\mathrm{erf}(x)+\dfrac{1}{\sqrt{\pi}}e^{-x^2}+C\)

    We take \[\begin{array}{ll} u=\mathrm{erf}(x) & dv=dx \\ du=\dfrac{2}{\sqrt{\pi}}e^{-x^2}\,dx \quad & v=x \end{array}\] Thus \[\begin{aligned} \int \mathrm{erf}(x)\,dx =x\,\mathrm{erf}(x)-\dfrac{2}{\sqrt{\pi}}\int xe^{-x^2}\,dx \end{aligned}\] To compute the remaining integral, we use the substitution \(z=-x^2\). Then \(dz=-2x\,dx\) and so: \[\begin{aligned} \int \mathrm{erf}(x)\,dx &=x\,\mathrm{erf}(x)+\dfrac{1}{\sqrt{\pi}}\int e^z\,dz \\ &=x\,\mathrm{erf}(x)+\dfrac{1}{\sqrt{\pi}}e^{-x^2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\,\mathrm{erf}(x)+\dfrac{1}{\sqrt{\pi}}e^{-x^2}\),   then \[ f'(x)=\mathrm{erf}(x)+\dfrac{2x}{\sqrt{\pi}}e^{-x^2}-\dfrac{2x}{\sqrt{\pi}}e^{-x^2} =\mathrm{erf}(x) \]

---

The following problems can all be done by substitution, but give them a try using parts.

34. \(\displaystyle \int 3x\sqrt{2x+1}\,dx\;\)

    Use the parts \(u=3x\) and \(dv=\sqrt{2x+1}\,dx\).

    \(\displaystyle \int 3x\sqrt{2x+1}\,dx =x(2x+1)^{3/2}-\dfrac{1}{5}(2x+1)^{5/2}+C\)

    We use the parts \[\begin{array}{ll} u=3x & dv=\sqrt{2x+1}\,dx \\ du=3\,dx \quad & v=\dfrac{1}{3}(2x+1)^{3/2} \end{array}\] (To find \(v\), we used the substitution \(z=2x+1\).) Then \[\begin{aligned} \int 3x\sqrt{2x+1}\,dx &=x(2x+1)^{3/2}-\int (2x+1)^{3/2}\,dx \\ &=x(2x+1)^{3/2}-\dfrac{1}{5}(2x+1)^{5/2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If  \(f(x)=x(2x+1)^{3/2}-\dfrac{1}{5}(2x+1)^{5/2}\),   then \[\begin{aligned} f'(x) &=(2x+1)^{3/2}+3x(2x+1)^{1/2}-(2x+1)^{3/2} \\ &=3x\sqrt{2x+1} \end{aligned}\]

35. \(\displaystyle \int x^2\sqrt{x+3}\,dx\)

    You will need to integrate by parts twice. Start with the parts \(u=x^2\) and \(dv=\sqrt{x+3}\,dx\).

    \(\begin{aligned}\displaystyle \int &x^2\sqrt{x+3}\,dx \\ &=\dfrac{2}{3}x^2(x+3)^{3/2}-\dfrac{8}{15}x(x+3)^{5/2} +\dfrac{16}{105}(x+3)^{7/2}+C \end{aligned}\)

    We let \[\begin{array}{ll} u=x^2 & dv=\sqrt{x+3}\,dx \\ du=2x\,dx \quad & v=\dfrac{2}{3}(x+3)^{3/2} \end{array}\] Then \[ \int x^2\sqrt{x+3}\,dx =\dfrac{2}{3}x^2(x+3)^{3/2}-\dfrac{4}{3}\int x(x+3)^{3/2}\,dx \] Next, we let \[\begin{array}{ll} u=x & dv=(x+3)^{3/2}\,dx \\ du=dx \quad & v=\dfrac{2}{5}(x+3)^{5/2} \end{array}\] So \[\begin{aligned} \int x^2\sqrt{x+3}\,dx &=\dfrac{2}{3}x^2(x+3)^{3/2} -\dfrac{4}{3}\left(\dfrac{2}{5}x(x+3)^{5/2} -\dfrac{2}{5}\int (x+3)^{5/2}\,dx\right) \\ &=\dfrac{2}{3}x^2(x+3)^{3/2}-\dfrac{8}{15}x(x+3)^{5/2} +\dfrac{8}{15}\dfrac{2}{7}(x+3)^{7/2}+C \\ &=\dfrac{2}{3}x^2(x+3)^{3/2}-\dfrac{8}{15}x(x+3)^{5/2} +\dfrac{16}{105}(x+3)^{7/2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{2}{3}x^2(x+3)^{3/2}-\dfrac{8}{15}x(x+3)^{5/2}+\dfrac{16}{105}(x+3)^{7/2}\),   then \[\begin{aligned} f'(x) &=\dfrac{4}{3}x(x+3)^{3/2}+x^2(x+3)^{1/2}-\dfrac{8}{15}(x+3)^{5/2} \\ &\quad-\dfrac{4}{3}x(x+3)^{3/2}+\dfrac{8}{15}(x+3)^{5/2} \\ &=x^2\sqrt{x+3} \end{aligned}\]

36. \(\displaystyle \int t\sqrt{t+2}\,dt\;\)

    \(\displaystyle \int t\sqrt{t+2}\,dt =\dfrac{2}{3}t(t+2)^{3/2}-\dfrac{4}{15}(t+2)^{5/2}+C\)

    We take the parts \[\begin{array}{ll} u=t & dv=\sqrt{t+2}\,dt \\ du=dt \quad & v=\dfrac{2}{3}(t+2)^{3/2} \end{array}\] Then: \[\begin{aligned} \int t\sqrt{t+2}\,dt &=\dfrac{2}{3}t(t+2)^{3/2} -\int \dfrac{2}{3}(t+2)^{3/2}\,dt \\ &=\dfrac{2}{3}t(t+2)^{3/2}-\dfrac{4}{15}(t+2)^{5/2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If  \(f(t)=\dfrac{2}{3}t(t+2)^{3/2}-\dfrac{4}{15}(t+2)^{5/2}\),   then \[ f'(t)=\dfrac{2}{3}(t+2)^{3/2}+t(t+2)^{1/2}-\dfrac{2}{3}(t+2)^{3/2} =t\sqrt{t+2} \]

37. \(\displaystyle \int x^2\sqrt{x-1}\,dx\)

    \(\displaystyle \int x^2\sqrt{x-1}\,dx =\dfrac{2}{3}x^2(x-1)^{3/2}-\dfrac{8}{15}x(x-1)^{5/2} +\dfrac{16}{105}(x-1)^{7/2}+C\)

    We use the parts \[\begin{array}{ll} u=x^2 & dv=\sqrt{x-1}\,dx \\ du=2x\,dx \quad & v=\dfrac{2}{3}(x-1)^{3/2} \end{array}\] Then: \[\begin{aligned} \int x^2\sqrt{x-1}\,dx &=\dfrac{2}{3}x^2(x-1)^{3/2} -\dfrac{4}{3}\int x(x-1)^{3/2}\,dx \end{aligned}\] We apply parts again using: \[\begin{array}{ll} u=x & dv=(x-1)^{3/2}\,dx \\ du=dx \quad & v=\dfrac{2}{5}(x-1)^{5/2} \end{array}\] Then: \[\begin{aligned} \int x^2\sqrt{x-1}\,dx &=\dfrac{2}{3}x^2(x-1)^{3/2} -\dfrac{4}{3}\left[\dfrac{2}{5}x(x-1)^{5/2} -\dfrac{2}{5}\int (x-1)^{5/2}\,dx\right] \\ &=\dfrac{2}{3}x^2(x-1)^{3/2} -\dfrac{8}{15}x(x-1)^{5/2}+\dfrac{8}{15}\int (x-1)^{5/2}\,dx \\ &=\dfrac{2}{3}x^2(x-1)^{3/2} -\dfrac{8}{15}x(x-1)^{5/2}+\dfrac{16}{105}(x-1)^{7/2}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If  \(f(x)=\dfrac{2}{3}x^2(x-1)^{3/2}-\dfrac{8}{15}x(x-1)^{5/2}+\dfrac{16}{105}(x-1)^{7/2}\),   then \[\begin{aligned} f'(x) &=\dfrac{4}{3}x(x-1)^{3/2}+x^2(x-1)^{1/2}-\dfrac{8}{15}(x-1)^{5/2} \\ &\quad-\dfrac{4}{3}x(x-1)^{3/2}+\dfrac{8}{15}(x-1)^{5/2} \\ &=x^2\sqrt{x-1} \end{aligned}\]

c. Definite Integrals

1

Use integration by parts to compute the following definite integrals. The formula for definite integrals is: \[ \int_a^b u\,dv=\left[u\,v\rule{0pt}{10pt}\right]_a^b-\int_a^b v\,du \] However, it is usually easier to just compute the indefinite integral and then evaluate at the limits. This also gives us a chance to check our intermediate work.

38. \(\displaystyle \int_0^1 xe^{4x}\,dx\)

    \(\displaystyle \int_0^1 xe^{4x}\,dx =\dfrac{3}{16}e^4+\dfrac{1}{16}\)

    We integrate by parts using: \[\begin{array}{ll} u=x & dv=e^{4x}\,dx \\ du=dx \quad & v=\dfrac{1}{4}e^{4x} \end{array}\] So: \[\begin{aligned} \int_0^1 xe^{4x}\,dx &=\left[\dfrac{1}{4}xe^{4x}\right]_0^1-\dfrac{1}{4}\int_0^1 e^{4x}\,dx\\ &=\dfrac{1}{4}e^{4}-\left[\dfrac{1}{16}e^{4x}\right]_0^1 \\ &=\dfrac{1}{4}e^{4}-\dfrac{1}{16}e^{4}+\dfrac{1}{16} \\ &=\dfrac{3}{16}e^{4}+\dfrac{1}{16} \end{aligned}\] Here we have used the fact that \(e^0=1\).

    lk 

    Alternatively, we can find the indefinite integral of \(\displaystyle \int xe^{4x}\,dx\): \[\begin{array}{ll} u=x & dv=e^{4x}\,dx \\ du=dx \quad & v=\dfrac{1}{4}e^{4x} \end{array}\] Then: \[\begin{aligned} \int xe^{4x}\,dx &=\dfrac{1}{4}xe^{4x}-\dfrac{1}{4}\int e^{4x}\,dx\\ &=\dfrac{1}{4}xe^{4x}-\dfrac{1}{16}e^{4x}+C \\ \end{aligned}\] Then we plug in the limits: \[\begin{aligned} \int_0^1 xe^{4x}\,dx &=\left[\dfrac{1}{4}xe^{4x}-\dfrac{1}{16}e^{4x}\right]_0^1 \\ &=\dfrac{1}{4}e^{4}-\dfrac{1}{16}e^{4}+\dfrac{1}{16} \\ &=\dfrac{3}{16}e^{4}+\dfrac{1}{16} \end{aligned}\] This method allows us to check the antiderivaive.

    lk 

    We check the indefinite integral by using the Product Rule. If   \(f(x)=\dfrac{1}{4}xe^{4x}-\dfrac{1}{16}e^{4x}\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{4}e^{4x}+xe^{4x}-\dfrac{1}{4}e^{4x} \\ &=xe^{4x} \end{aligned}\]

39. \(\displaystyle \int_0^{\pi/2} 2x\cos x\,dx\)

    \(\displaystyle \int_0^{\pi/2} 2x\cos x\,dx=\pi-2\)

    First, we find the indefinite integral of \(\displaystyle \int 2x\cos x\,dx\): \[\begin{array}{ll} u=2x & dv=\cos x\,dx \\ du=2\,dx \quad & v=\sin x \end{array}\] Then: \[\begin{aligned} \int 2x\cos x\,dx &=2x\sin x-\int 2\sin x\,dx \\ &=2x\sin x+2\cos x+C \\ \end{aligned}\] Now we plug in the limits: \[\begin{aligned} \int_0^{\pi/2} 2x\cos x\,dx &=\left[2x\sin x+2\cos x\dfrac{}{}\right]_0^{\pi/2} \\ &=\pi+0-0-2 \\ &=\pi-2 \end{aligned}\] Here we have used the facts that \(\sin\dfrac{\pi}{2}=1\) and \(\cos\dfrac{\pi}{2}=0\).

    lk 

    We check using the Product Rule on the indefinite integral of \(\displaystyle \int 2x\cos x\,dx\). If  \(f(x)=2x\sin x+2\cos x\),   then \[\begin{aligned} f'(x) &=2\sin x+2x\cos x-2\sin x \\ &=2x\cos x \end{aligned}\]

40. \(\displaystyle \int_{-2}^1 x^2e^x\,dx\)

    \(\displaystyle \int_{-2}^1 x^2e^x\,dx=e-10e^{-2}\)

    To find the indefinite integral \(\displaystyle \int x^2e^x\,dx\), we begin with the parts: \[\begin{array}{ll} u=x^2 & dv=e^x\,dx \\ du=2x\,dx \quad & v=e^x \end{array}\] So: \[\begin{aligned} \int x^2e^x\,dx &=x^2e^x-2\int xe^x\,dx \\ \end{aligned}\] Then we use the parts: \[\begin{array}{ll} u=x & dv=e^x\,dx \\ du=dx \quad & v=e^x \end{array}\] So: \[\begin{aligned} \int x^2e^x\,dx &=x^2e^x-2\left(xe^x-\int e^{x}\,dx\right) \\ &=x^2e^x-2xe^x+2e^{x}+C \\ \end{aligned}\] Finally, we evaluate at the limits: \[\begin{aligned} \int_{-2}^1 x^2e^x\,dx &=\left[\dfrac{}{}x^2e^x-2xe^x+2e^{x}\right]_{-2}^1 \\ &=(e-2e+2e)-(4e^{-2}+4e^{-2}+2e^{-2}) \\ &=e-10e^{-2} \end{aligned}\]

    lk 

    We check the indefinite integral using the Product Rule. If  \(f(x)=x^2e^x-2xe^x+2e^{x}\),   then \[\begin{aligned} f'(x) &=2xe^{x}+x^2e^{x}-2e^{x}-2xe^{x}+2e^{x} \\ &=x^2e^{x} \end{aligned}\]

41. \(\displaystyle \int_1^e x^3\ln x\,dx\)

    \(\displaystyle \int_1^e x^3\ln x\,dx =\dfrac{3}{16}e^4+\dfrac{1}{16}\)

    We first find the indefinite integral using the parts: \[\begin{array}{ll} u=\ln x & dv=x^3\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=\dfrac{1}{4}x^4 \end{array}\] Then: \[\begin{aligned} \int x^3\ln x\,dx &=\dfrac{1}{4}x^4\ln x-\int \dfrac{1}{4}x^3\,dx \\ &=\dfrac{1}{4}x^4\ln x-\dfrac{1}{16}x^4+C \end{aligned}\] Now we plug in the limits: \[\begin{aligned} \int_1^e x^3\ln x\,dx &=\left[\dfrac{1}{4}x^4\ln x-\dfrac{1}{16}x^4\right]_1^e \\ &=\dfrac{1}{4}e^4-\dfrac{1}{16}e^4-0+\dfrac{1}{16} \\ &=\dfrac{3}{16}e^4+\dfrac{1}{16} \end{aligned}\]

    lk 

    We check the indefinite integral by differentiating. If  \(f(x)=\dfrac{1}{4}x^4\ln x-\dfrac{1}{16}x^4\),   then \[\begin{aligned} f'(x) &=x^3\ln x+\dfrac{1}{4}x^4\dfrac{1}{x}-\dfrac{1}{4}x^3 \\ &=x^3\ln x \end{aligned}\]

42. \(\displaystyle \int_0^1 (x^2+2x)e^{2x}\,dx\)

    \(\displaystyle \int_0^1 (x^2+2x)e^{2x}\,dx =\dfrac{3}{4}e^2+\dfrac{1}{4}\)

    To find the indefinite integral, we begin with the parts: \[\begin{array}{ll} u=x^2+2x & dv=e^{2x}\,dx \\ du=(2x+2)\,dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] Then: \[\begin{aligned} \int (x^2+2x)e^{2x}\,dx &=(x^2+2x)\dfrac{1}{2}e^{2x}-\int \dfrac{1}{2}e^{2x}(2x+2)\,dx \\ &=\dfrac{1}{2}(x^2+2x)e^{2x}-\int (x+1)e^{2x}\,dx \end{aligned}\] Next, we use the parts: \[\begin{array}{ll} u=x+1 & dv=e^{2x}\,dx \\ du=dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] So: \[\begin{aligned} \int (x^2+2x)e^{2x}\,dx &=\dfrac{1}{2}(x^2+2x)e^{2x} -\left((x+1)\dfrac{1}{2}e^{2x}-\int \dfrac{1}{2}e^{2x}\,dx\right) \\ &=\dfrac{1}{2}(x^2+2x)e^{2x} -(x+1)\dfrac{1}{2}e^{2x}+\dfrac{1}{4}e^{2x}+C \\ &=\dfrac{1}{4}e^{2x}(2x^2+4x-2x-2+1)+C \\ &=\dfrac{1}{4}e^{2x}(2x^2+2x-1)+C \end{aligned}\] Then the definite integral is: \[\begin{aligned} \int_0^1 (x^2+2x)e^{2x}\,dx &=\left[\dfrac{1}{4}e^{2x}(2x^2+2x-1)\right]_0^1 \\ &=\dfrac{3}{4}e^2+\dfrac{1}{4} \end{aligned}\]

    lk 

    We check the indefinite integral using the Product Rule. If   \(f(x)=\dfrac{1}{4}e^{2x}(2x^2+2x-1)\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}e^{2x}(2x^2+2x-1)+\dfrac{1}{4}e^{2x}(4x+2) \\ &=\dfrac{1}{2}e^{2x}(2x^2+2x-1+2x+1) =e^{2x}(x^2+2x) \end{aligned}\]

43. \(\displaystyle \int_0^3 x\sqrt{x+1}\,dx\)

    \(\displaystyle \int_0^3 x\sqrt{x+1}\,dx =\dfrac{116}{15}\)

    We first find the indefinite integral of \(\displaystyle \int x\sqrt{x+1}\,dx\) by taking the parts: \[\begin{array}{ll} u=x & dv=(x+1)^{1/2}\,dx \\ du=\,dx \quad & v=\dfrac{2}{3}(x+1)^{3/2} \end{array}\] Then: \[\begin{aligned} \int x\sqrt{x+1}\,dx &=\dfrac{2}{3}x(x+1)^{3/2}-\int \dfrac{2}{3}(x+1)^{3/2}\,dx \\ &=\dfrac{2}{3}x(x+1)^{3/2}-\dfrac{4}{15}(x+1)^{5/2}+C \end{aligned}\] Then the definite integral is: \[\begin{aligned} \int_0^3 x\sqrt{x+1}\,dx &=\left[\dfrac{2}{3}x(x+1)^{3/2}-\dfrac{4}{15}(x+1)^{5/2}\right]_0^3 \\[3pt] &=\dfrac{2}{3}3(4)^{3/2}-\dfrac{4}{15}(4)^{5/2}-0+\dfrac{4}{15} \\ &=2(8)-\dfrac{4}{15}(32)+\dfrac{4}{15} \\[3pt] &=16-\dfrac{124}{15} = \dfrac{116}{15} \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{2}{3}x(x+1)^{3/2}-\dfrac{4}{15}(x+1)^{5/2}\),   then \[\begin{aligned} f'(x) &=\dfrac{2}{3}(x+1)^{3/2}+x(x+1)^{1/2}-\dfrac{2}{3}(x+1)^{3/2} \\ &=x\sqrt{x+1} \end{aligned}\]

    It is easier to do this integral by using the ordinary substitution \(u=x+1\). Then \(du=dx\) and \(x=u-1\). So: \[\begin{aligned} \int_0^3 &x\sqrt{x+1}\,dx =\int_1^4 (u-1)u^{1/2}\,du =\int_1^4 u^{3/2}-u^{1/2}\,du \\ &=\left[\dfrac{}{}\dfrac{2}{5}u^{5/2}-\dfrac{2}{3}u^{3/2}\right]_1^4 =\dfrac{2}{5}32-\dfrac{2}{3}8-\dfrac{2}{5}+\dfrac{2}{3} \\ &=\dfrac{62}{5}-\dfrac{14}{3} =\dfrac{116}{15} \end{aligned}\]

44. \(\displaystyle \int_{-1}^3 xe^{-4x}\,dx\)

    \(\displaystyle \int_{-1}^3 xe^{-4x}\,dx =-\,\dfrac{13}{16}e^{-12}-\dfrac{3}{16}e^4\)

    To find the indefinite integral, we take the parts: \[\begin{array}{ll} u=x & dv=e^{-4x}\,dx \\ du=dx \quad & v=-\,\dfrac{1}{4}e^{-4x} \end{array}\] Then: \[\begin{aligned} \int xe^{-4x}\,dx &=-\,\dfrac{1}{4}xe^{-4x}+\int \dfrac{1}{4}e^{-4x}\,dx \\ &=-\,\dfrac{1}{4}xe^{-4x}-\dfrac{1}{16}e^{-4x}+C \end{aligned}\] Then the definite integral is: \[\begin{aligned} \int_{-1}^3 xe^{-4x}\,dx &=\left[-\dfrac{1}{4}xe^{-4x}-\dfrac{1}{16}e^{-4x}\right]_{-1}^3 \\ &=\left[-\dfrac{3}{4}e^{-12}-\dfrac{1}{16}e^{-12}\right] -\left[\dfrac{1}{4}e^{4}-\dfrac{1}{16}e^{4}\right] \\ &=-\,\dfrac{13}{16}e^{-12}-\dfrac{3}{16}e^{4} \end{aligned}\]

    lk 

    We check the indefinite integral using the Product Rule. If   \(f(x)=-\,\dfrac{1}{4}xe^{-4x}-\dfrac{1}{16}e^{-4x}\),   then \[ f'(x) =-\,\dfrac{1}{4}e^{-4x}+xe^{-4x}+\dfrac{1}{4}e^{-4x} =xe^{-4x} \]

45. \(\displaystyle \int_1^e \ln x\,dx\)

    You should remember: \[ \int \ln x\,dx=x\ln x-x+C \]

    \(\displaystyle \int_1^e \ln x\,dx=1\)

    We remember: \[ \int \ln x\,dx=x\ln x-x+C \] Then: \[\begin{aligned} \int_1^e \ln x\,dx &=\left[\dfrac{}{}x\ln x-x\right]_1^e \\ &=(e\ln e-e)-(1\ln 1-1)=1 \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\ln x-x\),   then \[ f'(x) =\ln x+x\dfrac{1}{x}-1 =\ln x \]

46. \(\displaystyle \int_{-\sqrt{3} }^1\arctan x\,dx\)

    From a previous exercise (which you don't need to memorize): \[ \int \arctan x\,dx=x\arctan x-\dfrac{1}{2}\ln(1+x^2)+C \]

    \(\displaystyle \int_{-\sqrt{3} }^1\arctan x\,dx =\dfrac{1}{2}\ln 2+\dfrac{\pi}{4}-\dfrac{\pi\sqrt{3}}{3}\)

    From a previous exercise: \[ \int \arctan x\,dx=x\arctan x-\dfrac{1}{2}\ln(1+x^2)+C \] Then: \[\begin{aligned} \int_{-\sqrt{3}}^1 &\arctan x\,dx =\left[x\arctan x-\dfrac{1}{2}\ln(1+x^2)\right]_{-\sqrt{3}}^1 \\ &=\left(\arctan 1-\dfrac{1}{2}\ln 2\right)-\left(-\sqrt{3}\arctan (-\sqrt{3})-\dfrac{1}{2}\ln 4\right) \\ &=\dfrac{\pi}{4}-\dfrac{1}{2}\ln 2-\sqrt{3}\dfrac{\pi}{3}+\dfrac{1}{2}\ln 2^2 \\ &=\dfrac{\pi}{4}-\dfrac{1}{2}\ln 2-\dfrac{\sqrt{3}\pi}{3}+\ln 2 \\ &=\dfrac{1}{2}\ln 2+\dfrac{\pi}{4}-\dfrac{\sqrt{3}\pi}{3} \\ \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\arctan x-\dfrac{1}{2}\ln(1+x^2)\),   then \[ f'(x) =\arctan x+\dfrac{x}{1+x^2}-\dfrac{x}{1+x^2} =\arctan x \]

47. \(\displaystyle \int_0^{1/2} \arcsin 2x\,dx\)

    From a previous exercise on this page: \[ \int \arcsin 2x\,dx =x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}+C \]

    \(\displaystyle \int_0^{1/2} \arcsin 2x\,dx =\dfrac{\pi}{4}-\dfrac{1}{2}\)

    From a previous exercise on this page: \[ \int \arcsin 2x\,dx =x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}+C \] So: \[\begin{aligned} \int_0^{1/2} \arcsin 2x\,dx &=\left[x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}\right]_0^{1/2} \\ &=\left(\dfrac{1}{2}\arcsin 1+0\right)-\left(0+\dfrac{1}{2}\right) \\ &=\dfrac{\pi}{4}-\dfrac{1}{2} \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\arcsin 2x+\dfrac{1}{2}\sqrt{1-4x^2}\),   then \[ f'(x) =\arcsin 2x+\dfrac{2x}{\sqrt{1-4x^2}}-\dfrac{2x}{\sqrt{1-4x^2}} =\arcsin 2x \]

48. \(\displaystyle \int_{-2}^2 x\cos x\,dx\)

    \(\displaystyle \int_{-2}^2 x\cos x\,dx=0\)

    Let \[\begin{array}{ll} u=x & dv=\cos x\,dx \\ du=dx \quad & v=\sin x \end{array}\] Then \[\begin{aligned} \int x\cos x\,dx &=x\sin x-\int \sin x\,dx \\ &=x\sin x+\cos x+C \end{aligned}\] We plug in to get the definite integral: \[\begin{aligned} \int_{-2}^2 x\cos x\,dx &=\left[x\sin x+\cos x\rule{0pt}{10pt}\right]_{-2}^2 \\ &=[2\sin 2+\cos 2]-\left[-2\sin(-2)+\cos(-2)\right] \\ &=2\sin 2+\cos 2-2\sin 2-\cos 2 \\ &=0 \end{aligned}\] We have used the facts that \(\sin(-x)=-\sin x\) and \(\cos(-x)=\cos x\) for all \(x\).

    lk 

    We check using the Product Rule. If   \(f(x)=x\sin x+\cos x\),   then \[ f'(x) =\sin x+x\cos x-\sin x =x\cos x \]

The answer should have been obvious. Notice that \(f(x)=x\cos x\) is an odd function (i.e. \(f(-x)=-f(x)\)) and the interval \([-2,2]\) is symmetric about \(0\). So the area above the \(x\)-axis must cancel with the area below. Look at the graph. So the integral must be \(0\).



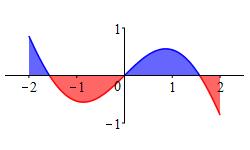
49. \(\displaystyle \int_1^2 x\ln|x|\,dx\)

    Let \(u=\ln|x|\) and \(dv=x\,dx\).

    \(\displaystyle \int_1^2 x\ln|x|\,dx =2\ln 2-\dfrac{3}{4}\)

    First we find the indfeinite integral. Let \[\begin{array}{ll} u=\ln|x| & dv=x\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=\dfrac{x^2}{2} \end{array}\] Then \[\begin{aligned} \int x\ln|x|\,dx &=\dfrac{x^2}{2}\ln|x|-\int \dfrac{x}{2}\,dx \\ &=\dfrac{x^2}{2}\ln|x|-\dfrac{x^2}{4}+C \end{aligned}\] Now we plug in the limits to find the definite integral \[\begin{aligned} \int_1^2 x\ln|x|\,dx &=\left[\dfrac{x^2}{2}\ln|x|-\dfrac{x^2}{4}\right]_1^2 \\ &=\dfrac{4}{2}\ln|2|-\dfrac{4}{4}-\dfrac{1}{2}\ln|1|+\dfrac{1}{4} \\ &= 2\ln 2-\dfrac{3}{4} \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{x^2}{2}\ln|x|-\dfrac{x^2}{4}\),   then \[ f'(x) =x\ln|x|+\dfrac{x^2}{2}\dfrac{1}{x}-\dfrac{x}{2} =x\ln x \]

50. \(\displaystyle \int_0^3 \ln|x+1|\,dx\)

    Use integration by parts with \(u=\ln|x+1|\) and \(dv=dx\).
    Alternatively, use a substitution and remember the antiderivative of \(\ln x\).

    \(\displaystyle \int_0^3 \ln|x+1|\,dx =4\ln4-3\)

    Let \[\begin{array}{ll} u=\ln|x+1| & dv=dx \\ du=\dfrac{1}{x+1}\,dx \quad & v=x \end{array}\] Then \[\begin{aligned} \int \ln|x+1|\,dx &=x\ln|x+1|-\int \dfrac{x}{x+1}\,dx \end{aligned}\] To compute the integral, we can use the long division of polynomials to get: \[\begin{aligned} \int \ln|x+1|\,dx &=x\ln|x+1|-\int 1-\dfrac{1}{x+1}\,dx \\ &=x\ln|x+1|-x+\ln|x+1|+C \\ \end{aligned}\] We plug in the limits to get the definite integral \[\begin{aligned} \int_0^3 \ln|x+1|\,dx &=\left[\dfrac{}{}x\ln|x+1|+\ln|x+1|-x\right]_0^3 \\ &=(3\ln 4+\ln 4-3)-(0\ln 1+\ln 1-0) \\ &=4\ln 4-3 \end{aligned}\]

    Alternatively, we make the substitution \(u=x+1\) and \(du=dx\): \[\begin{aligned} \int_0^3 \ln|x+1|\,dx &=\int_1^4 \ln|u|\,du =\left[\dfrac{}{}u\ln|u|-u\right]_1^4 \\ &=(4\ln4-4)-(1\ln1-1) =4\ln4-3 \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\ln|x+1|+\ln|x+1|-x\),   then \[\begin{aligned} f'(x) &=\ln|x+1|+\dfrac{x}{x+1}+\dfrac{1}{x+1}-1 \\ &=\ln|x+1|+\dfrac{x+1}{x+1}-1 =\ln|x+1| \end{aligned}\]

51. \(\displaystyle \int_0^1 x\ln|x+1|\,dx\)

    Let \(u=\ln|x+1|\) and \(dv=x\,dx\).

    \(\displaystyle \int_0^1 x\ln|x+1|\,dx =\dfrac{1}{4}\)

    We choose the parts: \[\begin{array}{ll} u=\ln|x+1| & dv=x\,dx \\ du=\dfrac{1}{x+1}\,dx \quad & v=\dfrac{x^2}{2} \end{array}\] Then \[\begin{aligned} \int x\ln|x+1|\,dx &=\dfrac{x^2}{2}\ln|x+1|-\dfrac{1}{2}\int \dfrac{x^2}{x+1}\,dx \end{aligned}\] To compute the remaining integral, we use polynomial long division: \[\begin{aligned} \int x\ln|x+1|\,dx &=\dfrac{x^2}{2}\ln|x+1|-\dfrac{1}{2}\int x-1+\dfrac{1}{x+1}\,dx \\ &=\dfrac{x^2}{2}\ln|x+1|-\dfrac{1}{2}\left(\dfrac{x^2}{2}-x+\ln|x+1|\right)+C \\ &=\dfrac{x^2-1}{2}\ln|x+1|-\dfrac{x^2}{4}+\dfrac{x}{2}+C \end{aligned}\] Finally, we plug in the limits: \[\begin{aligned} \int_0^1 x\ln|x+1|\,dx &=\left[\dfrac{x^2-1}{2}\ln|x+1|-\dfrac{x^2}{4}+\dfrac{x}{2}\right]_0^1 \\ &=\left(0\ln2-\dfrac{1}{4}+\dfrac{1}{2}\right)-0 =\dfrac{1}{4} \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{x^2-1}{2}\ln|x+1|-\dfrac{x^2}{4}+\dfrac{x}{2}\),   then \[\begin{aligned} f'(x) &=x\ln|x+1|+\dfrac{x^2-1}{2(x+1)}-\dfrac{x}{2}+\dfrac{1}{2} \\ &=x\ln|x+1|+\dfrac{1}{2}(x-1)-\dfrac{x}{2}+\dfrac{1}{2} \\ &=x\ln|x+1| \end{aligned}\]

52. \(\displaystyle \int_2^4 (x-2)e^{x+1}\,dx\)

    Let \(u=x-2\) and \(dv=e^{x+1}\,dx\).

    \(\displaystyle \int_2^4 (x-2)e^{x+1}\,dx =e^5+e^3\)

    We take the parts \[\begin{array}{ll} u=x-2 & dv=e^{x+1}\,dx \\ du=dx \quad & v=e^{x+1} \end{array}\] Then \[\begin{aligned} \int \left(x-2\right)e^{x+1}\,dx &=\left(x-2\right)e^{x+1}-\int e^{x+1}\,dx \\ &=(x-2)e^{x+1}-e^{x+1}+C \\ &=(x-3)e^{x+1}+C \end{aligned}\] We evaluate at the limits \[\begin{aligned} \int_2^4 \left(x-2\right)e^{x+1}\,dx &=\left[\rule{0pt}{10pt}(x-3)e^{x+1}\right]_2^4 \\ &=e^5+e^3 \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=(x-3)e^{x+1}\),   then \[ f'(x) =e^{x+1}+(x-3)e^{x+1}=(x-2)e^{x+1} \]

53. \(\displaystyle \int_0^4 3x\sqrt{2x+1}\,dx\)

    There is no reason to use integration by parts. Just make the substitution \(u=2x+1\).

    \(\displaystyle \int_0^4 3x\sqrt{2x+1}\,dx =\dfrac{298}{5}\)

    It is easiest to just make the subsitution \(u=2x+1\) and \(du=2\,dx\). Then \(\dfrac{1}{2}\,du=dx\) and \(x=\dfrac{u-1}{2}\). So: \[\begin{aligned} \int 3x\sqrt{2x+1}\,dx &=\dfrac{3}{2}\int \dfrac{u-1}{2}\sqrt{u}\,du \\ &=\dfrac{3}{4}\int u^{3/2}-u^{1/2}\,du \\ &=\dfrac{3}{4}\left(\dfrac{2}{5}u^{5/2}-\dfrac{2}{3}u^{3/2}\right)+C \\ &=\dfrac{3}{10}(2x+1)^{5/2}-\dfrac{1}{2}(2x+1)^{3/2}+C \end{aligned}\] We now plug in the limits: \[\begin{aligned} \int_0^4 3x\sqrt{2x+1}\,dx &=\left[\dfrac{3}{10}(2x+1)^{5/2}-\dfrac{1}{2}(2x+1)^{3/2}\right]_0^4 \\ &=\left[\dfrac{3}{10}9^{5/2}-\dfrac{1}{2}9^{3/2}\right] -\left[\dfrac{3}{10}-\dfrac{1}{2}\right] \\ &=\dfrac{3}{10}243-\dfrac{1}{2}27-\dfrac{3}{10}+\dfrac{1}{2} \\ &=\dfrac{3}{10}242-\dfrac{1}{2}26=\dfrac{363}{5}-13=\dfrac{298}{5} \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x) =\dfrac{3}{10}(2x+1)^{5/2}-\dfrac{1}{2}(2x+1)^{3/2}\),   then \[\begin{aligned} f'(x) &=\dfrac{3}{4}(2x+1)^{3/2}2-\dfrac{3}{4}(2x+1)^{1/2}2 \\ &=\dfrac{3}{2}(2x+1)^{1/2}(2x+1-1) =3x\sqrt{2x+1} \end{aligned}\]

54. \(\displaystyle \int_1^4 \dfrac{\ln x}{\sqrt{x}}\,dx\)

    Let \(u=\ln x\) and \(dv=x^{-1/2}\,dx\)

    \(\displaystyle \int_1^4 \dfrac{\ln x}{\sqrt{x}}\,dx =4\ln 4-4\)

    Let: \[\begin{array}{ll} u=\ln x & dv=x^{-1/2}\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=2x^{1/2} \end{array}\] Then: \[\begin{aligned} \int \dfrac{\ln x}{\sqrt{x}}\,dx &=2x^{1/2}\ln x-\int 2x^{-1/2}\,dx \\ &=2x^{1/2}\ln x-4x^{1/2}+C \end{aligned}\] We plug in the limits: \[\begin{aligned} \int_1^4 \dfrac{\ln x}{\sqrt{x}}\,dx &=\left[2x^{1/2}\ln x-4x^{1/2}\right]_1^4 \\ &=2(4)^{1/2}\ln 4-4(4)^{1/2}-2\ln 1+4 \\ &=4\ln4-4 \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=2x^{1/2}\ln x-4x^{1/2}\),   then \[ f'(x)=x^{-1/2}\ln x+2x^{-1/2}-2x^{-1/2}=\dfrac{\ln x}{\sqrt{x}} \]

---

55. Find the average value of the function \(f(x)=x\sin x\) over the interval \([0,\pi]\).

    

    Remember that the formula for average value is: \[ f_\text{ave}=\dfrac{1}{b-a}\int_a^b f(x)\,dx \]

    \(f_\text{ave}=1\)

    Let: \[\begin{array}{ll} u=x & dv=\sin x\,dx \\ du=dx \quad & v=-\cos x \end{array}\] Then \[\begin{aligned} \int x\sin x\,dx &=-x\cos x+\int \cos x\,dx \\ &=-x\cos x+\sin x+C \end{aligned}\] So: \[\begin{aligned} \int_0^\pi x\sin x\,dx &=\left[\dfrac{}{}-x\cos x+\sin x\right]_0^\pi \\ &=(-\pi\cos\pi)-(0)=\pi \end{aligned}\] and: \[ f_\text{ave}=\dfrac{1}{\pi}\int_0^\pi x\sin x\,dx=1 \]

    lk 

    We check using the Product Rule. If   \(f(x)=-x\cos x+\sin x\),   then \[ f'(x)=-\cos x+x\sin x+\cos x=x\sin x \]

56. A company's total sales of gallons of sludge is \(P(t)\) where \(t\) is the number of weeks since the sludge product was introduced. Further, the rate of sales is \(P'(t)=3000t^2 e^{-2t}\) gallons per week. How many gallons were sold during the first six weeks?

    This is another application of the Fundamental Theorem. The integral of the rate of sales gives total sales. Hence, we have \(\displaystyle P(t)=\int_0^t 3000x^2 e^{-2x}\,dx\) and we want to know \(\displaystyle P(6)=\int_0^6 3000x^2 e^{-2x}\,dx\).

    \(P=750-63750e^{-12}\approx749.6\) gallons

    First read the hint. To compute \(\displaystyle \int 3000x^2 e^{-2x}\,dx\), we let: \[\begin{array}{ll} u=3000x^2 & dv=e^{-2x}\,dx \\ du=6000x\,dx \quad & v=-\,\dfrac{1}{2}e^{-2x} \end{array}\] Then \[\begin{aligned} \int 3000x^2 e^{-2x}\,dx &=-1500x^2e^{-2x}+\int 3000xe^{-2x}\,dx \\ \end{aligned}\] For the remaining integral, take: \[\begin{array}{ll} u=3000x & dv=e^{-2x}\,dx \\ du=3000\,dx \quad & v=-\,\dfrac{1}{2}e^{-2x} \end{array}\] Then \[\begin{aligned} \int 3000x^2 e^{-2x}\,dx &=-1500x^2e^{-2x}-1500xe^{-2x}+\int 1500e^{-2x}\,dx \\ &=-1500x^2e^{-2x}-1500xe^{-2x}-750e^{-2x}+C \\ &=(-1500x^2-1500x-750)e^{-2x}+C \\ \end{aligned}\] So the sales in the first \(6\) weeks are \[\begin{aligned} P(6) &=\int_0^6 3000x^2 e^{-2x}\,dx \\ &=\left[\dfrac{}{}(-1500x^2-1500x-750)e^{-2x}\right]_0^6 \\ &=(-1500\cdot6^2-1500\cdot6-750)e^{-12}-(-750) \\ &=750-63750e^{-12}\approx749.6 \text{gallons} \end{aligned}\]

    lk 

    We check the indefinite integral by using the Product Rule. If   \(f(x)=(-1500x^2-1500x-750)e^{-2x}\),   then \[\begin{aligned} f'(x) &=(-3000x-1500)e^{-2x}-2(-1500x^2-1500x-750)e^{-2x} \\ &=(-3000x-1500+3000x^2+3000x+1500)e^{-2x} \\ &=3000x^2e^{-2x} \end{aligned}\]

d. Recurrence of the Integral

1

2

Use integration by parts to compute the following integrals:

57. \(\displaystyle \int e^{2x}\cos x\,dx\)

    Either take \(u=e^{2x}\) for both applications of integration by parts, or take \(u=\cos x\) for the first integration by parts and \(u=\sin x\) for the second one.

    \(\displaystyle \int e^{2x}\cos x\,dx =\dfrac{2}{5}e^{2x}\cos x+\dfrac{1}{5}e^{2x}\sin x+C\)

    This is a product of a trig function and an exponential. So LAPTE tells us that \(u\) should be the trig function. So we take the parts: \[\begin{array}{ll} u=\cos x & dv=e^{2x}\,dx \\ du=-\sin x\,dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] Hence: \[ \int e^{2x}\cos x\,dx =\dfrac{1}{2}e^{2x}\cos x+\dfrac{1}{2}\int e^{2x}\sin x\,dx \] Now, we take the parts: \[\begin{array}{ll} u=\sin x & dv=e^{2x}\,dx \\ du=\cos x\,dx \quad & v=\dfrac{1}{2}e^{2x} \end{array}\] So: \[\begin{aligned} \int &e^{2x}\cos x\,dx =\dfrac{1}{2}e^{2x}\cos x \\ &\quad+\dfrac{1}{2}\left(\dfrac{1}{2}e^{2x}\sin x-\dfrac{1}{2}\int e^{2x}\cos x\,dx\right) \\ &=\dfrac{1}{2}e^{2x}\cos x \\ &\quad+\dfrac{1}{4}e^{2x}\sin x-\dfrac{1}{4}\int e^{2x}\cos x\,dx \end{aligned}\] Finally, we add \(\displaystyle \dfrac{1}{4}\int e^{2x}\cos x\,dx\) to both sides and multiply by \(\dfrac{4}{5}\): \[\begin{aligned} \dfrac{5}{4}\int e^{2x}\cos x\,dx &=\dfrac{1}{2}e^{2x}\cos x+\dfrac{1}{4}e^{2x}\sin x+K \\ \int e^{2x}\cos x\,dx &=\dfrac{2}{5}e^{2x}\cos x+\dfrac{1}{5}e^{2x}\sin x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{2}{5}e^{2x}\cos x+\dfrac{1}{5}e^{2x}\sin x\),   then \[\begin{aligned} f'(x) &=\dfrac{4}{5}e^{2x}\cos x-\dfrac{2}{5}e^{2x}\sin x \\ &\quad+\dfrac{2}{5}e^{2x}\sin x+\dfrac{1}{5}e^{2x}\cos x \\ &=e^{2x}\cos x \end{aligned}\] which is the original integrand.

    In the solution, \(dv=e^{2x}\,dx\) in both integrations by parts. It can also be done taking \(u=e^{2x}\) in both integrations by parts, as follows:

    First, we take the parts: \[\begin{array}{ll} u=e^{2x} & dv=\cos x\,dx \\ du=2e^{2x}\,dx \quad & v=\sin x \end{array}\] Hence: \[ \int e^{2x}\cos x\,dx =e^{2x}\sin x-2\int e^{2x}\sin x\,dx \] Next, we take the parts: \[\begin{array}{ll} u=e^{2x} & dv=\sin x\,dx \\ du=2e^{2x}\,dx \quad & v=-\cos x \end{array}\] So: \[\begin{aligned} \int e^{2x}\cos x\,dx &=e^{2x}\sin x-2\left(-e^{2x}\cos x+2\int e^{2x}\cos x\,dx\right) \\ &=e^{2x}\sin x+2e^{2x}\cos x-4\int e^{2x}\cos x\,dx \end{aligned}\] Finally, we add \(\displaystyle 4\int e^{2x}\cos x\,dx\) to both sides and divide by \(5\): \[\begin{aligned} 5\int e^{2x}\cos x\,dx &=e^{2x}\sin x+2e^{2x}\cos x+K \\ \int e^{2x}\cos x\,dx &=\dfrac{1}{5}e^{2x}\sin x+\dfrac{2}{5}e^{2x}\cos x+C \end{aligned}\]

58. \(\displaystyle \int e^{-x}\cos x\,dx\)

    Take \(u=e^{-x}\) for both applications of integration by parts.

    \(\displaystyle \int e^{-x}\cos x\,dx =\dfrac{1}{2}e^{-x}\sin x-\dfrac{1}{2}e^{-x}\cos x+C\)

    We first take the parts: \[\begin{array}{ll} u=e^{-x} & dv=\cos x\,dx \\ du=-e^{-x}\,dx \quad & v=\sin x \end{array}\] Then: \[ \int e^{-x}\cos x\,dx =e^{-x}\sin x+\int e^{-x}\sin x\,dx \] We now take the parts \[\begin{array}{ll} u=e^{-x} & dv=\sin x\,dx \\ du=-e^{-x}\,dx \quad & v=-\cos x \end{array}\] Hence \[ \int e^{-x}\cos x\,dx =e^{-x}\sin x-e^{-x}\cos x-\int e^{-x}\cos x\,dx \] Now add \(\displaystyle \int e^{-x}\cos x\,dx\) to both sides and divide by \(2\): \[\begin{aligned} 2\int e^{-x}\cos x\,dx &=e^{-x}\sin x-e^{-x}\cos x+K \\ \int e^{-x}\cos x\,dx &=\dfrac{1}{2}e^{-x}\sin x-\dfrac{1}{2}e^{-x}\cos x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{1}{2}e^{-x}\sin x-\dfrac{1}{2}e^{-x}\cos x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{1}{2}e^{-x}\sin x+\dfrac{1}{2}e^{-x}\cos x \\ &\quad+\dfrac{1}{2}e^{-x}\cos x+\dfrac{1}{2}e^{-x}\sin x \\ &=e^{-x}\cos x \end{aligned}\] which agrees with the original integrand.

    In the solution, \(u=e^{-x}\) in both integrations by parts. It can also be done taking \(dv=e^{-x}\,dx\) in both integrations by parts.

59. \(\displaystyle \int e^x\cos 3x\,dx\)

    \(\displaystyle \int e^x\cos 3x\,dx =\dfrac{1}{10}e^{x}\cos 3x+\dfrac{3}{10}e^{x}\sin 3x+C\)

    We first take the parts: \[\begin{array}{ll} u=\cos 3x & dv=e^{x}\,dx \\ du=-3\sin 3x\,dx \quad & v=e^{x} \end{array}\] Then: \[ \int e^{x}\cos 3x\,dx =e^{x}\cos 3x+3\int e^{x}\sin 3x\,dx \] We now take the parts \[\begin{array}{ll} u=\sin 3x & dv=e^{x}\,dx \\ du=3\cos 3x\,dx \quad & v=e^{x} \end{array}\] Hence \[\begin{aligned} \int &e^{x}\cos 3x\,dx =e^{x}\cos 3x \\ &\quad+3\left(e^{x}\sin 3x-3\int e^{x}\cos 3x\,dx\right) \end{aligned}\] We now add \(\displaystyle 9\int e^{x}\cos 3x\,dx\) to both sides and divide by \(10\): \[\begin{aligned} 10\int e^{x}\cos 3x\,dx &=e^{x}\cos 3x+3e^{x}\sin 3x+K \\ \int e^{x}\cos 3x\,dx &=\dfrac{1}{10}e^{x}\cos 3x+\dfrac{3}{10}e^{x}\sin 3x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{1}{10}e^{x}\cos 3x+\dfrac{3}{10}e^{x}\sin 3x\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{10}e^x\cos 3x-\dfrac{3}{10}e^x\sin 3x \\ &\quad+\dfrac{3}{10}e^x\sin 3x+\dfrac{9}{10}e^x\cos 3x \\ &=e^x\cos 3x \end{aligned}\]

    In the solution, \(dv=e^x\,dx\) in both integrations by parts. It can also be done taking \(u=e^x\) in both integrations by parts.

60. \(\displaystyle \int e^{2x}\sin 2x\,dx\)

    Either take \(u=e^{2x}\) for both applications of integration by parts, or take \(u=\sin 2x\) for the first integration by parts and \(u=\cos 2x\) for the second one.

    \(\displaystyle \int e^{2x}\sin 2x\,dx =-\,\dfrac{1}{4}e^{2x}\cos 2x+\dfrac{1}{4}e^{2x}\sin 2x+C\)

    We first take the parts: \[\begin{array}{ll} u=e^{2x} & dv=\sin 2x\,dx \\ du=2e^{2x}\,dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\] Then: \[ \int e^{2x}\sin 2x\,dx =-\,\dfrac{1}{2}e^{2x}\cos 2x+\int e^{2x}\cos 2x\,dx \] We now take the parts: \[\begin{array}{ll} u=e^{2x} & dv=\cos 2x\,dx \\ du=2e^{2x}\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\] Hence \[ \int e^{2x}\sin 2x\,dx =-\,\dfrac{1}{2}e^{2x}\cos 2x+\dfrac{1}{2}e^{2x}\sin 2x-\int e^{2x}\sin 2x\,dx \] We now add \(\displaystyle \int e^{2x}\sin 2x\,dx\) to both sides and divide by \(2\): \[\begin{aligned} 2\int e^{x}\cos 2x\,dx &=-\,\dfrac{1}{2}e^{2x}\cos 2x+\dfrac{1}{2}e^{2x}\sin 2x+K \\ \int e^{2x}\cos 2x\,dx &=-\,\dfrac{1}{4}e^{2x}\cos 2x+\dfrac{1}{4}e^{2x}\sin 2x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{1}{4}e^{2x}\cos 2x+\dfrac{1}{4}e^{2x}\sin 2x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{1}{2}e^{2x}\cos 2x+\dfrac{1}{2}e^{2x}\sin 2x \\ &\quad+\dfrac{1}{2}e^{2x}\sin 2x+\dfrac{1}{2}e^{2x}\cos 2x \\ &=e^{2x}\sin 2x \end{aligned}\]

    In the solution, \(u=e^{2x}\) in both integrations by parts. It can also be done taking \(dv=e^{2x}\,dx\) in both integrations by parts.

61. \(\displaystyle \int e^{-5x}\sin 3x\,dx\)

    \(\displaystyle \int e^{-5x}\sin 3x\,dx =-\,\dfrac{3}{34}e^{-5x}\cos 3x-\dfrac{5}{34}e^{-5x}\sin 3x+C\)

    We first take the parts: \[\begin{array}{ll} u=e^{-5x} & dv=\sin 3x\,dx \\ du=-5e^{-5x}\,dx \quad & v=-\,\dfrac{1}{3}\cos 3x \end{array}\] Then: \[ \int e^{-5x}\sin 3x\,dx =-\,\dfrac{1}{3}e^{-5x}\cos 3x-\dfrac{5}{3}\int e^{-5x}\cos 3x\,dx \] We now take the parts again \[\begin{array}{ll} u=e^{-5x} & dv=\cos 3x\,dx \\ du=-5e^{-5x}\,dx \quad & v=\dfrac{1}{3}\sin 3x \end{array}\] Hence \[\begin{aligned} \int &e^{-5x}\sin 3x\,dx =-\,\dfrac{1}{3}e^{-5x}\cos 3x \\ &-\dfrac{5}{3}\left(\dfrac{1}{3}e^{-5x}\sin 3x +\dfrac{5}{3}\int e^{-5x}\sin 3x\,dx\right) \end{aligned}\] Now add \(\displaystyle \dfrac{25}{9}\int e^{-5x}\sin 3x\,dx\) to both sides and multiply by \(\dfrac{9}{34}\): \[\begin{aligned} \dfrac{34}{9}\int e^{-5x}\sin 3x\,dx &=-\,\dfrac{1}{3}e^{-5x}\cos 3x-\dfrac{5}{9}e^{-5x}\sin 3x+K \\ \int e^{-5x}\sin 3x\,dx &=-\,\dfrac{3}{34}e^{-5x}\cos 3x-\dfrac{5}{34}e^{-5x}\sin 3x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{3}{34}e^{-5x}\cos 3x-\dfrac{5}{34}e^{-5x}\sin 3x\),   then \[\begin{aligned} f'(x) &=\dfrac{15}{34}e^{-5x}\cos 3x+\dfrac{9}{34}e^{-5x}\sin 3x \\ &\quad+\dfrac{25}{34}e^{-5x}\sin 3x-\dfrac{15}{34}e^{-5x}\cos 3x \\ &=e^{-5x}\sin 3x \end{aligned}\]

    In the solution, \(u=e^{-5x}\) in both integrations by parts. It can also be done taking \(dv=e^{-5x}\,dx\) in both integrations by parts.

62. \(\displaystyle \int \sin 3x\cos 2x\,dx\)

    Either take \(u=\sin 3x\) for the first applications of integration by parts and \(u=\cos 3x\) for the second one, or take \(u=\cos 2x\) for the first integration by parts and \(u=\sin 2x\) for the second one. The important thing is to keep the coefficient of \(x\) the same both times, or else the second integration will undo the first.

    \(\displaystyle \int \sin 3x\cos 2x\,dx =-\,\dfrac{2}{5}\sin 3x\sin 2x-\dfrac{3}{5}\cos 3x\cos 2x+C\)

    We first take the parts: \[\begin{array}{ll} u=\sin 3x & dv=\cos 2x\,dx \\ du=3\cos 3x\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\] Then: \[ \int \sin 3x\cos 2x\,dx =\dfrac{1}{2}\sin 3x\sin 2x-\dfrac{3}{2}\int \cos 3x\sin 2x\,dx \] We now take the parts \[\begin{array}{ll} u=\cos 3x & dv=\sin 2x\,dx \\ du=-3\sin 3x\,dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\] Hence \[\begin{aligned} \int &\sin 3x\cos 2x\,dx=\dfrac{1}{2}\sin 3x\sin 2x \\ &-\dfrac{3}{2}\left(-\,\dfrac{1}{2}\cos 3x\cos 2x -\dfrac{3}{2}\int \sin 3x\cos 2x\,dx\right) \end{aligned}\] Now subtract \(\displaystyle \dfrac{9}{4}\int \sin 3x\cos 2x\,dx\) from both sides and multiply by \(-\,\dfrac{4}{5}\): \[\begin{aligned} -\,\dfrac{5}{4}\int \sin 3x\cos 2x\,dx &=\dfrac{1}{2}\sin 3x\sin 2x+\dfrac{3}{4}\cos 3x\cos 2x+K \\ \int \sin 3x\cos 2x\,dx &=-\,\dfrac{2}{5}\sin 3x\sin 2x-\dfrac{3}{5}\cos 3x\cos 2x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{2}{5}\sin 3x\sin 2x-\dfrac{3}{5}\cos 3x\cos 2x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{6}{5}\cos 3x\sin 2x-\dfrac{4}{5}\sin 3x\cos 2x \\ &\quad+\dfrac{9}{5}\sin 3x\cos 2x+\dfrac{6}{5}\cos 3x\sin 2x \\ &=\sin 3x\cos 2x \end{aligned}\]

    Another method of computing this integral is in the chapter on Trig Integrals.

63. \(\displaystyle \int xe^x\sin x\,dx\)   (This one is tough.)

    Start with \(u=x\) and \(dv=e^x\sin x\,dx\). But then you will need to work hard to find \(\displaystyle v=\int e^x\sin x\,dx\).

    \(\displaystyle \int xe^x\sin x\,dx =\dfrac{x}{2}e^x\sin x+\left(-\,\dfrac{x}{2}+\dfrac{1}{2}\right)e^x\cos x+C\)

    We first take the parts \[\begin{array}{ll} u=x & dv=e^x\sin x\,dx \\ du=dx \quad & v=\text{???} \end{array}\] To find \(\displaystyle v=\int e^x\sin x\,dx\) it is necessary to integrate by parts twice and solve for the recurring integral. In fact, this was done in an example on a previous page. The result was: \[\begin{aligned} v=\int e^x\sin x\,dx =\dfrac{1}{2}e^x\sin x-\dfrac{1}{2}e^x\cos x \qquad\qquad(1) \end{aligned}\] Hence \[\begin{aligned} \int xe^x\sin x\,dx &=x\left(\dfrac{1}{2}e^x\sin x-\dfrac{1}{2}e^x\cos x\right) \\ &\quad -\int \left(\dfrac{1}{2}e^x\sin x-\dfrac{1}{2}e^x\cos x\right)\,dx \\ &=\dfrac{x}{2}e^x\sin x-\dfrac{x}{2}e^x\cos x \\ &\quad -\dfrac{1}{2}\int e^x\sin x\,dx+\dfrac{1}{2}\int e^x\cos x\,dx \end{aligned}\] Each of the remaining integrals must be integrated by the recurrence method. The first is equation \((1)\) above. The second is \[ \int e^x\cos x\,dx =\dfrac{1}{2}e^x\sin x+\dfrac{1}{2}e^x\cos x \qquad\qquad(2) \] (Check this by differentiating.) Putting it all together gives \[\begin{aligned} \int xe^x\sin x\,dx &=\dfrac{x}{2}e^x\sin x-\dfrac{x}{2}e^x\cos x \\ &\quad-\dfrac{1}{2}\left(\dfrac{1}{2}e^x\sin x-\dfrac{1}{2}e^x\cos x\right) \\ &\quad+\dfrac{1}{2}\left(\dfrac{1}{2}e^x\sin x+\dfrac{1}{2}e^x\cos x\right)+C \\ &=\dfrac{x}{2}e^x\sin x+\left(-\,\dfrac{x}{2}+\dfrac{1}{2}\right)e^x\cos x+C \end{aligned}\]

    lk 

    We check using the Product Rule. Note that each term is the product of \(3\) functions! If   \(f(x)=\dfrac{x}{2}e^x\sin x+\left(-\,\dfrac{x}{2}+\dfrac{1}{2}\right)e^x\cos x\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}e^{x}\sin x+\dfrac{x}{2}e^{x}\sin x+\dfrac{x}{2}e^{x}\cos x \\ &\quad-\dfrac{1}{2}e^{x}\cos x+\left(-\,\dfrac{x}{2}+\dfrac{1}{2}\right)e^x\cos x-\left(-\,\dfrac{x}{2}+\dfrac{1}{2}\right)e^x\sin x \\ &=\dfrac{1}{2}e^{x}\sin x+\dfrac{x}{2}e^{x}\sin x+\dfrac{x}{2}e^{x}\cos x \\ &\quad-\dfrac{1}{2}e^{x}\cos x-\dfrac{x}{2}e^x\cos x+\dfrac{1}{2}e^x\cos x+\dfrac{x}{2}e^x\sin x-\dfrac{1}{2}e^x\sin x \\ &=xe^x\sin x \end{aligned}\]

64. \[ \int \sin^n x\,dx =-\,\dfrac{1}{n}\sin^{n-1}x\cos x+\dfrac{n-1}{n}\int \sin^{n-2}x\,dx \] The reduction formula was derived in an exercise in the text.

    1. Use the reduction formula to compute \(\displaystyle \int \sin^2 x\,dx\).

       \(\displaystyle \int \sin^2 x\,dx =-\,\dfrac{1}{2}\sin x\cos x+\dfrac{1}{2}x+C\)

       Plugging \(n=2\) into the reduction formula, we get \[\begin{aligned} \int \sin^2 x\,dx &=-\,\dfrac{1}{2}\sin x\cos x+\dfrac{1}{2}\int 1\,dx \\ &=-\,\dfrac{1}{2}\sin x\cos x+\dfrac{1}{2}x+C \end{aligned}\]

       lk 

       We check using the Product Rule. If   \(f(x)=-\,\dfrac{1}{2}\sin x\cos x+\dfrac{1}{2}x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{1}{2}\cos^2 x+\dfrac{1}{2}\sin^2 x+\dfrac{1}{2} \\ &=\dfrac{1}{2}\left(1-\cos^2 x\right)+\dfrac{1}{2}\sin^2 x \end{aligned}\] We use the Pythagorean Identity for Sine and Cosine to subsitute \(1-\cos^2 x=\sin^2 x\) \[\begin{aligned} &=\dfrac{1}{2}\left(\sin^2 x\right)+\dfrac{1}{2}\sin^2 x \\ &=\sin^2 x \end{aligned}\]

       Another method of computing this integral is in the chapter on Trig Integrals.

    2. Use the reduction formula to compute \(\displaystyle \int \sin^4 x\,dx\).

       \(\displaystyle \int \sin^4 x\,dx =-\,\dfrac{1}{4}\sin^3 x\cos x-\dfrac{3}{8}\sin x\cos x+\dfrac{3}{8}x+C\)

       Plugging \(n=4\) into the reduction formula, we get: \[ \int \sin^4 x\,dx =-\,\dfrac{1}{4}\sin^3 x\cos x+\dfrac{3}{4}\int \sin^2x\,dx \] For the last integral, we substitute in the formula for \(\displaystyle \int \sin^2 x\,dx\): \[\begin{aligned} \int \sin^4 x\,dx &=-\,\dfrac{1}{4}\sin^3 x\cos x +\dfrac{3}{4}\left(-\,\dfrac{1}{2}\sin x\cos x+\dfrac{1}{2}x\right)+C \\ &=-\,\dfrac{1}{4}\sin^3 x\cos x-\dfrac{3}{8}\sin x\cos x+\dfrac{3}{8}x+C \end{aligned}\]

       lk 

       We check using the Product Rule, To get everything in terms of \(\sin x\), we use the Pythagorean Identity to subsitute \(\cos^2 x=1-\sin^2 x\). If   \(f(x)=-\,\dfrac{1}{4}\sin^3 x\cos x-\dfrac{3}{8}\sin x\cos x+\dfrac{3}{8}x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{3}{4}\sin^2 x\cos^2 x+\dfrac{1}{4}\sin^4 x-\dfrac{3}{8}\cos^2 x+\dfrac{3}{8}\sin^2 x+\dfrac{3}{8} \\ &=-\,\dfrac{3}{4}\sin^2 x(1-\sin^2 x)+\dfrac{1}{4}\sin^4 x-\dfrac{3}{8}(1-\sin^2 x)+\dfrac{3}{8}\sin^2 x+\dfrac{3}{8} \\ &=-\,\dfrac{3}{4}\sin^2 x+\dfrac{3}{4}\sin^4 x+\dfrac{1}{4}\sin^4 x-\dfrac{3}{8}+\dfrac{3}{8}\sin^2 x+\dfrac{3}{8}\sin^2 x+\dfrac{3}{8} \\ &=\sin^4 x \end{aligned}\]

       Another method of computing this integral is in the chapter on Trig Integrals.

65. \[ \int \cos^n x\,dx =\dfrac{1}{n}\cos^{n-1}x\sin x+\dfrac{n-1}{n}\int \cos^{n-2}x\,dx \] The reduction formula was derived in an example in the text.

    1. Use the reduction formula to compute \(\displaystyle \int \cos^3 x\,dx\).

       \(\displaystyle \int \cos^3 x\,dx =\dfrac{1}{3}\cos^2 x\sin x+\dfrac{2}{3}\sin x+C\)

       Plugging in \(n=3\) into the reduction formula, we get \[\begin{aligned} \int \cos^3 x\,dx &=\dfrac{1}{3}\cos^2 x\sin x+\dfrac{2}{3}\int \cos x\,dx \\ &=\dfrac{1}{3}\cos^2 x\sin x+\dfrac{2}{3}\sin x+C \end{aligned}\]

       lk 

       We check using the Product Rule and the Pythagorean Identity for Sine and Cosine to subsitute \(\sin^2 x=1-\cos^2 x\). If   \(f(x)=\dfrac{1}{3}\cos^2 x\sin x+\dfrac{2}{3}\sin x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{2}{3}\cos x\sin^2 x+\dfrac{1}{3}\cos^3 x+\dfrac{2}{3}\cos x \\ &=-\,\dfrac{2}{3}\cos x\left(1-\cos^2 x\right)+\dfrac{1}{3}\cos^3 x +\dfrac{2}{3}\cos x\\ &=\dfrac{2}{3}\cos^3 x+\dfrac{1}{3}\cos^3 x \\ &=\cos^3 x \end{aligned}\]

       Another method of computing this integral is in the chapter on Trig Integrals.

    2. Use the reduction formula to compute \(\displaystyle \int \cos^5 x\,dx\).

       \(\displaystyle \int\cos^5x\,dx =\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\sin x+C\)

       Plugging in \(n=5\) into the reduction formula, we get \[ \int\cos^5x\,dx =\dfrac{1}{5}\cos^4 x\sin x+\dfrac{4}{5}\int\cos^3x\,dx \] Now we substitute the result for \(\int\cos^3x\,dx\): \[\begin{aligned} \int\cos^5x\,dx &=\dfrac{1}{5}\cos^4 x\sin x +\dfrac{4}{5}\left(\dfrac{1}{3}\cos^2 x\sin x+\dfrac{2}{3}\sin x\right)+C \\ &=\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\sin x+C \end{aligned}\]

       We check using the Product Rule.
       If   \(f(x)=\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\sin x\),   then \[\begin{aligned} f'(x) &=\left(-\,\dfrac{4}{5}\cos^3 x\sin x-\dfrac{8}{15}\cos x\sin x\right)\sin x \\ &\quad+\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\cos x \\ &=-\,\left(\dfrac{4}{5}\cos^3 x+\dfrac{8}{15}\cos x\right)\sin^2 x \\ &\quad+\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\cos x \\ &=-\,\left(\dfrac{4}{5}\cos^3 x+\dfrac{8}{15}\cos x\right)(1-\cos^2 x) \\ &\quad+\left(\dfrac{1}{5}\cos^4 x +\dfrac{4}{15}\cos^2 x+\dfrac{8}{15}\right)\cos x \\ &=-\,\dfrac{4}{5}\cos^3 x-\dfrac{8}{15}\cos x +\dfrac{4}{5}\cos^5 x+\dfrac{8}{15}\cos^3 x \\ &\quad+\dfrac{1}{5}\cos^5 x +\dfrac{4}{15}\cos^3 x+\dfrac{8}{15}\cos x \\ &=\cos^5 x \end{aligned}\]

66. \[ \int \ln^n x\,dx=x\ln^n x-n\int \ln^{n-1} x\,dx \]

    1. Derive the reduction formula.

       Use integration by parts with \(u=\ln^n x\) and \(dv=dx\).

       We use the parts \[\begin{array}{ll} u=\ln^n x & dv=dx \\ du=\dfrac{n\ln^{n-1} x}{x}\,dx \quad & v=x \end{array}\] Hence: \[ \int \ln^n x\,dx =x\ln^n x-n\int \ln^{n-1} x\,dx \] which is the reduction formula.

       lk 

       We check using the Product Rule and the first FTC. If   \(\displaystyle f(x)=x\ln^n x-n\int \ln^{n-1} x\,dx\),   then \[\begin{aligned} f'(x) &=\ln^n x+x n\dfrac{\ln^{n-1} x}{x}-n\ln^{n-1} x \\ &=\ln^n x \end{aligned}\]

    2. Use the reduction formula to compute \(\displaystyle \int \ln^3 x\,dx\).

       \(\displaystyle \int \ln^3 x\,dx =x\ln^3 x-3x\ln^2 x+6x\ln x-6x+C\)

       We use the reduction formula three times: \[\begin{aligned} \int \ln^3 x\,dx &=x\ln^3 x-3\int \ln^2 x\,dx \\ &=x\ln^3 x-3\left(x\ln^2 x-2\int \ln x\,dx\right) \\ &=x\ln^3 x-3x\ln^2 x+6\left(x\ln x-\int 1\,dx\right) \\ &=x\ln^3 x-3x\ln^2 x+6x\ln x-6x+C \end{aligned}\]

       lk 

       We check using the Product Rule . If   \(f(x)=x\ln^3 x-3x\ln^2 x+6x\ln x-6x\),   then \[\begin{aligned} f'(x) &=\ln^3 x+x3\ln^2x\,\dfrac{1}{x}-3\ln^2 x-3x2\ln x\,\dfrac{1}{x} \\ &\quad+6\ln x+6x\,\dfrac{1}{x}-6 \\ &=\ln^3 x \end{aligned}\]

67. \[ \int \sec^n x\,dx =\dfrac{1}{n-1}\sec^{n-2} x\tan x +\dfrac{n-2}{n-1}\int \sec^{n-2}x\,dx \]

    1. Derive the reduction formula.

       Use integration by parts with \(u=\sec^{n-2} x\) and \(dv=\sec^2 x\,dx\).

       We use the parts \[\begin{array}{ll} u=\sec^{n-2} x & dv=\sec^2 x\,dx \\ du=(n-2)\sec^{n-3}x\sec x\tan x\,dx \quad & v=\tan x \end{array}\] Hence: \[\begin{aligned} \int \sec^n x\,dx &=\sec^{n-2} x\tan x \\ &\quad-(n-2)\int \sec^{n-2} x\tan^2 x\,dx \end{aligned}\] In the remaining integral, we use the identity \(\tan^2 x=\sec^2 x-1\), distribute the secants and split the integral into two parts: \[\begin{aligned} \int &\sec^n x\,dx =\sec^{n-2} x\tan x \\ &\qquad\qquad\quad-(n-2)\int \sec^{n-2} x(\sec^2 x-1)\,dx \\ &=\sec^{n-2} x\tan x \\ &\quad-(n-2)\int \sec^n x\,dx+(n-2)\int \sec^{n-2}x\,dx \end{aligned}\] The integral \(\int \sec^n x\,dx\) recurs on the right. So we add \((n-2)\int \sec^n x\,dx\) to both sides and then divide by \(n-1\): \[\begin{aligned} (n-1)\int \sec^n x\,dx &=\sec^{n-2} x\tan x+(n-2)\int\sec^{n-2}x\,dx \\ \end{aligned}\] \[\begin{aligned} \int \sec^n x\,dx &=\dfrac{1}{n-1}\sec^{n-2} x\tan x+\dfrac{n-2}{n-1}\int \sec^{n-2} x\,dx \end{aligned}\]

       lk 

       We check using the Product Rule, the first FTC and the Pythagorean Identity \(\tan^2 x+1=\sec^2 x\). If   \(\displaystyle f(x)=\dfrac{1}{n-1}\sec^{n-2} x\tan x +\dfrac{n-2}{n-1}\int \sec^{n-2} x\,dx\),   then \[\begin{aligned} f'(x) &=\dfrac{n-2}{n-1}\sec^{n-2} x\tan^2 x+\dfrac{1}{n-1}\sec^n x +\dfrac{n-2}{n-1}\sec^{n-2} x \\ &=\dfrac{n-2}{n-1}\sec^{n-2} x\left(\tan^2 x+1\right) +\dfrac{1}{n-1}\sec^n x \\ &=\dfrac{n-2}{n-1}\sec^{n-2} x\left(\sec^2 x\right) +\dfrac{1}{n-1}\sec^n x \\ &=\dfrac{n-2}{n-1}\sec^n x+\dfrac{1}{n-1}\sec^n x \\ &=\dfrac{n-1}{n-1}\sec^n x=\sec^n x \end{aligned}\]

    2. Use the reduction formula to compute \(\displaystyle \int \sec^4 x\,dx\).

       \(\displaystyle \int \sec^4 x\,dx =\dfrac{1}{3}\sec^2 x\tan x+\dfrac{2}{3}\tan x+C\)

       Plugging \(n=4\) into the reduction formula, we get: \[\begin{aligned} \int \sin^4 x\,dx &=\dfrac{1}{3}\sec^2 x\tan x+\dfrac{2}{3}\int \sec^2 x\,dx \\ &=\dfrac{1}{3}\sec^2 x\tan x+\dfrac{2}{3}\tan x+C \end{aligned}\]

       lk 

       We check using the Product Rule and the Pythagorean Identity \(\tan^2 x+1=\sec^2 x\). If   \(f(x)=\dfrac{1}{3}\sec^{2} x\tan x+\dfrac{2}{3}\tan x\),   then \[\begin{aligned} f'(x) &=\dfrac{2}{3}\sec^2 x\tan^2 x+\dfrac{1}{3}\sec^4 x+\dfrac{2}{3}\sec^2 x \\ &=\dfrac{2}{3}\sec^2 x\left(\tan^2 x+1\right)+\dfrac{1}{3}\sec^4 x \\ &=\dfrac{2}{3}\sec^2 x\left(\sec^2 x\right)+\dfrac{1}{3}\sec^4 x \\ &=\dfrac{2}{3}\sec^4 x+\dfrac{1}{3}\sec^4 x \\ &=\sec^4 x \end{aligned}\]

    3. Use the reduction formula to compute \(\displaystyle \int \sec^3 x\,dx\).
       Read the hint!

       You will need the integral: \[ \int \sec x\,dx=\ln|\sec x+\tan x|+C \] This integral will be derived in the chapter on Trig Integrals. However, it can be easily checked by differentiating: \[\begin{aligned} \dfrac{d}{dx}\ln|\sec x+\tan x| &=\dfrac{1}{\sec x+\tan x}(\sec x\tan x+\sec^2 x) \\[5pt] &=\dfrac{\sec x(\tan x+\sec x)}{\sec x+\tan x} =\sec x \end{aligned}\]

       \(\displaystyle \int \sec^3 x\,dx =\dfrac{1}{2}\sec x\tan x+\dfrac{1}{2}\ln|\sec x+\tan x|+C\)

       Plugging \(n=3\) into the reduction formula, we get: \[\begin{aligned} \int \sin^3 x\,dx &=\dfrac{1}{2}\sec x\tan x+\dfrac{1}{2}\int \sec x\,dx \\ &=\dfrac{1}{2}\sec x\tan x+\dfrac{1}{2}\ln|\sec x+\tan x|+C \end{aligned}\]

       py 

       We check using the Product Rule and the Pythagorean Identity \(\tan^2 x=\sec^2 x-1\). If   \(f(x)=\dfrac{1}{2}\sec x\tan x+\dfrac{1}{2}\ln|\sec x+\tan x|\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}\sec x\tan^2 x+\dfrac{1}{2}\sec^3 x+\dfrac{1}{2}\sec x \\ &=\dfrac{1}{2}\sec x(\sec^2 x-1)+\dfrac{1}{2}\sec^3 x+\dfrac{1}{2}\sec x \\ &=\sec^3 x \end{aligned}\] where we have used \(\dfrac{d}{dx}\ln|\sec x+\tan x|=\sec x\). (See the hint.)

Review Exercises

Evaluate using any appropriate method.

68. \(\displaystyle \int x^3 e^x\,dx\)

    Apply integration by parts three times.

    \(\displaystyle \int x^3e^x\,dx =x^3e^x-3x^2e^x+6xe^x-6e^x+C\)

    First, using the parts:   \(\begin{array}{ll} u=x^3 & dv=e^x\,dx \\ du=3x^2\,dx \quad & v=e^x \end{array}\) \[ \int x^3e^x\,dx=x^3e^x-3\int x^2e^x\,dx \] Second, using the parts:   \(\begin{array}{ll} u=x^2 & dv=e^x\,dx \\ du=2x\,dx \quad & v=e^x \end{array}\) \[\begin{aligned} \int e^3e^x\,dx &=e^3e^x-3\left(x^2e^x-2\int xe^x\,dx\right) \\ &=e^3e^x-3x^2e^x+6\int xe^x\,dx \end{aligned}\] Finally, using the parts:   \(\begin{array}{ll} u=x & dv=e^x\,dx \\ du=dx \quad & v=e^x \end{array}\) \[\begin{aligned} \int e^3e^x\,dx &=e^3e^x-3x^2e^x+6\left(xe^x-\int e^x\,dx\right) \\ &=e^3e^x-3x^2e^x+6xe^x-6e^x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x^3e^x-3x^2e^x+6xe^x-6e^x\),   then \[\begin{aligned} f'(x) &=3x^2e^x+x^3e^x-6xe^x-3x^2e^x+6e^x+6xe^x-6e^x \\ &=x^3e^x \end{aligned}\]

69. \(\displaystyle \int x^2\cos 2x\,dx\)

    Apply integration by parts twice.

    \(\displaystyle \int x^2\cos 2x\,dx =\dfrac{x^2}{2}\sin 2x+\dfrac{x}{2}\cos 2x-\dfrac{1}{4}\sin 2x+C\)

    First, using the parts:   \(\begin{array}{ll} u=x^2 & dv=\cos 2x\,dx \\ du=2x\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\) \[ \int x^2\cos 2x\,dx =\dfrac{x^2}{2}\sin 2x-\int x\sin 2x\,dx \] Then, using the parts:   \(\begin{array}{ll} u=x & dv=\sin 2x\,dx \\ du=dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\) \[\begin{aligned} \int x^2\cos 2x\,dx &=\dfrac{x^2}{2}\sin 2x-\left(-\,\dfrac{x}{2}\cos 2x +\dfrac{1}{2}\int \cos 2x\,dx\right) \\ &=\dfrac{x^2}{2}\sin 2x+\dfrac{x}{2}\cos 2x-\dfrac{1}{4}\sin 2x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{x^2}{2}\sin 2x+\dfrac{x}{2}\cos 2x-\dfrac{1}{4}\sin 2x\),   then \[\begin{aligned} f'(x) &=x\sin 2x+x^2\cos 2x+\dfrac{1}{2}\cos 2x-x\sin 2x-\dfrac{1}{2}\cos 2x \\ &=x^2\cos 2x \end{aligned}\]

70. \(\displaystyle \int x^2e^{12x}\,dx\)

    Apply integration by parts twice.

    \(\displaystyle \int x^2e^{12x}\,dx =\dfrac{x^2}{12}e^{12x}-\dfrac{x}{72}e^{12x}+\dfrac{1}{864}e^{12x}+C\)

    First, using the parts:   \(\begin{array}{ll} u=x^2 & dv=e^{12x}\,dx \\ du=2x\,dx \quad & v=\dfrac{1}{12}e^{12x} \end{array}\) \[ \int x^2e^{12x}\,dx =\dfrac{x^2}{12}e^{12x}-\dfrac{1}{6}\int xe^{12x}\,dx \] Then, using the parts:   \(\begin{array}{ll} u=x & dv=e^{12x}\,dx \\ du=\,dx \quad & v=\dfrac{1}{12}e^{12x} \end{array}\) \[\begin{aligned} \int x^2e^{12x}\,dx &=\dfrac{x^2}{12}e^{12x}-\dfrac{1}{6}\left(\dfrac{x}{12}e^{12x} -\dfrac{1}{12}\int e^{12x}\,dx\right) \\ &=\dfrac{x^2}{12}e^{12x}-\dfrac{x}{72}e^{12x}+\dfrac{1}{864}e^{12x}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=\dfrac{x^2}{12}e^{12x}-\dfrac{x}{72}e^{12x}+\dfrac{1}{864}e^{12x}\),   then \[\begin{aligned} f'(x) &=\dfrac{x}{6}e^{12x}+x^2e^{12x}-\dfrac{1}{72}e^{12x}-\dfrac{x}{6}e^{12x} +\dfrac{1}{72}e^{12x} \\ &=x^2e^{12x} \end{aligned}\]

71. \(\displaystyle \int x^2\sin 5x\,dx\)

    \(\displaystyle \int x^2\sin 5x\,dx =-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2x}{25}\sin 5x+\dfrac{2}{125}\cos 5x+C\)

    First, using the parts:   \(\begin{array}{ll} u=x^2 & dv=\sin 5x\,dx \\ du=2x\,dx \quad & v=-\,\dfrac{1}{5}\cos 5x \end{array}\) \[ \int x^2\sin 5x\,dx =-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2}{5}\int x\cos 5x\,dx \] Then, using the parts:   \(\begin{array}{ll} u=x & dv=\cos 5x\,dx \\ du=\,dx \quad & v=\dfrac{1}{5}\sin 5x \end{array}\) \[\begin{aligned} \int x^2\sin 5x\,dx &=-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2}{5}\left(\dfrac{x}{5}\sin 5x -\dfrac{1}{5}\int \sin 5x\,dx \right) \\ &=-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2}{5}\left(\dfrac{x}{5}\sin 5x +\dfrac{1}{25}\cos 5x\right)+C \\ &=-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2x}{25}\sin 5x+\dfrac{2}{125}\cos 5x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{x^2}{5}\cos 5x+\dfrac{2x}{25}\sin 5x+\dfrac{2}{125}\cos 5x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{2x}{5}\cos 5x+x^2\sin 5x+\dfrac{2}{25}\sin 5x+\dfrac{2x}{5}\cos 5x -\dfrac{2}{25}\sin 5x \\ &=x^2\sin 5x \end{aligned}\]

72. \(\displaystyle \int (x-1)^2e^{-x}\,dx\)

    \(\displaystyle \int (x-1)^2e^{-x}\,dx=-(x^2+1)e^{-x}+C \)

    First, using the parts:   \(\begin{array}{ll} u=(x-1)^2 & dv=e^{-x}\,dx \\ du=2(x-1)\,dx \quad & v=-e^{-x} \end{array}\) \[ \int (x-1)^2e^{-x}\,dx =-(x-1)^2e^{-x}+2\int (x-1)e^{-x}\,dx \] Then, using the parts:   \(\begin{array}{ll} u=(x-1) & dv=e^{-x}\,dx \\ du=dx \quad & v=-e^{-x} \end{array}\) \[\begin{aligned} \int (x-1)^2e^{-x}\,dx &=-(x-1)^2e^{-x}+2\left(-(x-1)e^{-x}+\int e^{-x}\,dx\right) \\ &=-(x-1)^2e^{-x}-2(x-1)e^{-x}-2e^{-x}+C\\ &=(-x^2+2x-1-2x+2-2)e^{-x}+C\\ &=-(x^2+1)e^{-x}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-(x^2+1)e^{-x}\),   then \[\begin{aligned} f'(x) &=-2xe^{-x}+(x^2+1)e^{-x} \\ &=(x^2-2x+1)e^{-x} \\ &=(x-1)^2e^{-x} \end{aligned}\]

73. \(\displaystyle \int x^3\sin 2x\,dx\)

    \(\begin{aligned} \int &x^3\sin 2x\,dx \\ &=-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3x^2}{4}\sin 2x +\dfrac{3x}{4}\cos 2x-\dfrac{3}{8}\sin 2x+C \end{aligned}\)

    First, using the parts:   \(\begin{array}{ll} u=x^3 & dv=\sin 2x\,dx \\ du=3x^2\,dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\) \[ \int x^3\sin 2x\,dx =-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3}{2}\int x^2\cos 2x\,dx \] Second, using the parts:   \(\begin{array}{ll} u=x^2 & dv=\cos 2x\,dx \\ du=2x\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\) \[\begin{aligned} \int x^3\sin 2x\,dx &=-\,\dfrac{x^3}{2}\cos 2x +\dfrac{3}{2}\left(\dfrac{x^2}{2}\sin 2x-\int x\sin 2x\,dx\right) \\ &=-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3x^2}{4}\sin 2x-\dfrac{3}{2}\int x\sin 2x\,dx \end{aligned}\] Finally, using the parts:   \(\begin{array}{ll} u=x & dv=\sin 2x\,dx \\ du=dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\) \[\begin{aligned} \int x^3\sin 2x\,dx &=-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3x^2}{4}\sin 2x \\ &\quad-\dfrac{3}{2}\left(-\,\dfrac{x}{2}\cos 2x+\dfrac{1}{2}\int\cos 2x\,dx\right) \\ &=-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3x^2}{4}\sin 2x \\ &\quad+\dfrac{3x}{4}\cos 2x-\dfrac{3}{8}\sin 2x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{x^3}{2}\cos 2x+\dfrac{3x^2}{4}\sin 2x+\dfrac{3x}{4}\cos 2x-\dfrac{3}{8}\sin 2x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{3x^2}{2}\cos 2x+x^3\sin 2x+\dfrac{3x}{2}\sin 2x+\dfrac{3x^2}{2}\cos 2x \\ &\quad+\dfrac{3}{4}\cos 2x-\dfrac{3x}{2}\sin 2x-\dfrac{3}{4}\cos 2x \\ &=x^3\sin 2x \end{aligned}\]

74. \(\displaystyle \int\dfrac{\ln 2x}{x^2}\,dx\)

    Let \(u=\ln 2x\) and \(dv=\dfrac{1}{x^2}\,dx\).

    \(\displaystyle \int\dfrac{\ln 2x}{x^2}\,dx =-\,\dfrac{\ln 2x}{x}-\dfrac{1}{x}+C\)

    We use the parts \[\begin{array}{ll} u=\ln 2x & dv=\dfrac{1}{x^2}\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=-\,\dfrac{1}{x} \end{array}\] Hence: \[\begin{aligned} \int \dfrac{\ln 2x}{x^2}\,dx &=-\,\dfrac{\ln 2x}{x}+\int \dfrac{1}{x^2}\,dx \\ &=-\,\dfrac{\ln 2x}{x}-\dfrac{1}{x}+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-x^{-1}\ln 2x-x^{-1}\),   then \[\begin{aligned} f'(x) &=x^{-2}\ln 2x-x^{-2}+x^{-2} \\ &=x^{-2}\ln 2x=\dfrac{\ln 2x}{x^2} \end{aligned}\]

75. \(\displaystyle \int \arctan 5x\,dx\)

    \(\displaystyle \int \arctan 5x\,dx =x\arctan 5x-\dfrac{1}{10}\ln(1+25x^2)+C\)

    Take \[\begin{array}{ll} u=\arctan 5x & dv=dx \\ du=\dfrac{5}{1+25x^2}\,dx \quad & v=x \end{array}\] Thus \[ \int \arctan 5x\,dx=x\arctan 5x-\int \dfrac{5x}{1+25x^2}\,dx \] To compute the second integral, use the substitution \(z=1+25x^2\). Then \(dz=50x\,dx\) and \(5x\,dx=\dfrac{1}{10}\,dz\). Thus: \[\begin{aligned} \int \arctan 5x\,dx &=x\arctan 5x-\dfrac{1}{10}\int \dfrac{1}{z}\,dz \\ &=x\arctan 5x-\dfrac{1}{10}\ln z+C \\ &=x\arctan 5x-\dfrac{1}{10}\ln(1+25x^2)+C \end{aligned}\]

    If you remember (You are not expected to remember this.) \[ \int \arctan u\,du =u\arctan u-\dfrac{1}{2}\ln(1+u^2)+C \] then the substitution \(u=5x\) gives: \[\begin{aligned} \int \arctan 5x\,dx &=\dfrac{1}{5}\int \arctan u\,du \\ &=\dfrac{1}{5}\left(u\arctan u-\dfrac{1}{2}\ln(1+u^2)\right)+C \\ &=x\arctan 5x-\dfrac{1}{10}\ln(1+25x^2)+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=x\arctan 5x-\dfrac{1}{10}\ln(1+25x^2)\),   then \[\begin{aligned} f'(x) &=\arctan 5x+\dfrac{5x}{1+25x^2}-\dfrac{1}{10}\dfrac{50x}{1+25x^2} \\ &=\arctan 5x \end{aligned}\]

76. \(\displaystyle \int_{-\sqrt{3}}^1 \arctan x\,dx\)

    Recall or rederive: \[ \int \arctan x=x\arctan x-\dfrac{1}{2}\ln(1+x^2)+C \]

    \(\displaystyle \int_{-\sqrt{3}}^1 \arctan x\,dx =\dfrac{\pi}{4}-\dfrac{\pi\sqrt{3}}{3}+\dfrac{1}{2}\ln 2\)

    Recall or rederive: \[ \int \arctan x=x\arctan x-\dfrac{1}{2}\ln(1+x^2)+C \] Then: \[\begin{aligned} \int_{-\sqrt{3}}^1 \arctan x\,dx &=\left[x\arctan x-\dfrac{1}{2}\ln(1+x^2)\right]_{-\sqrt{3}}^1 \\ &=\left(\arctan 1-\dfrac{1}{2}\ln 2\right) -\left(-\sqrt{3}\arctan(-\sqrt{3})-\dfrac{1}{2}\ln 4\right) \\ &=\dfrac{\pi}{4}-\dfrac{\pi\sqrt{3}}{3}+\dfrac{1}{2}\ln 2 \end{aligned}\] where we have used \(\ln4=2\ln2\),   \(\arctan 1=\dfrac{\pi}{4}\) and \(\arctan(-\sqrt{3})=-\,\dfrac{\pi}{3}\).

    lk 

77. \(\displaystyle \int_{-1}^1 xe^x\,dx\)

    \(\displaystyle \int_{-1}^1 xe^x\,dx =2e^{-1}\)

    Let: \[\begin{array}{ll} u=x & dv=e^x\,dx \\ du=dx \quad & v=e^x \end{array}\] Then: \[\begin{aligned} \int xe^x\,dx &=xe^x-\int e^x\,dx \\ &=xe^x-e^x+C \end{aligned}\] We plug in the limits: \[\begin{aligned} \int_{-1}^1 xe^x\,dx &=\left[\dfrac{}{}xe^x-e^x\right]_{-1}^1 \\ &=(e-e)-(-e^{-1}-e^{-1}) =2e^{-1} \end{aligned}\]

    lk 

    If   \(f(x)=xe^x-e^x\),   then   \(f'(x)=e^x+xe^x-e^x=xe^x\) as desired.

78. \(\displaystyle \int e^{3x}\sin 2x\,dx\)

    Integrate by parts twice and then solve for the integral.

    \(\displaystyle \int e^{3x}\sin 2x\,dx =-\,\dfrac{2}{13}e^{3x}\cos 2x+\dfrac{3}{13}e^{3x}\sin 2x+C\)

    We first take the parts: \[\begin{array}{ll} u=e^{3x} & dv=\sin 2x\,dx \\ du=3e^{3x}\,dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\] Hence: \[ \int e^{3x}\sin 2x\,dx =-\,\dfrac{1}{2}e^{3x}\cos 2x+\dfrac{3}{2}\int e^{3x}\cos 2x\,dx \] Now we take the parts: \[\begin{array}{ll} u=e^{3x} & dv=\cos 2x\,dx \\ du=3e^{3x}\,dx \quad & v=\dfrac{1}{2}\sin 2x \end{array}\] Hence: \[\begin{aligned} \int e^{3x}\sin 2x\,dx &=-\,\dfrac{1}{2}e^{3x}\cos 2x \\ &\quad+\dfrac{3}{2}\left(\dfrac{1}{2}e^{3x}\sin 2x -\dfrac{3}{2}\int e^{3x}\sin 2x\,dx\right) \\ &=-\,\dfrac{1}{2}e^{3x}\cos 2x+\dfrac{3}{4}e^{3x}\sin 2x \\ &\quad-\dfrac{9}{4}\int e^{3x}\sin 2x\,dx \end{aligned}\] The integral \(\displaystyle \int e^{3x}\sin 2x\,dx\) appears on both sides. So we solve for it. \[\begin{aligned} \left(1+\dfrac{9}{4}\right)\int e^{3x}\sin 2x\,dx &=-\,\dfrac{1}{2}e^{3x}\cos 2x+\dfrac{3}{4}e^{3x}\sin 2x+K \\ \int e^{3x}\sin 2x\,dx &=-\,\dfrac{2}{13}e^{3x}\cos 2x+\dfrac{3}{13}e^{3x}\sin 2x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If \(f(x)=-\,\dfrac{2}{13}e^{3x}\cos 2x+\dfrac{3}{13}e^{3x}\sin 2x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{6}{13}e^{3x}\cos 2x+\dfrac{4}{13}e^{3x}\sin 2x \\ &\quad+\dfrac{9}{13}e^{3x}\sin 2x+\dfrac{6}{13}e^{3x}\cos 2x \\ &=e^{3x}\sin 2x \end{aligned}\]

    In the solution, \(u=e^{3x}\) in both integrations by parts. It can also be done taking \(dv=e^{3x}\,dx\) in both integrations by parts.

79. \(\displaystyle \int e^{-x}\sin x\,dx\)

    \(\displaystyle \int e^{-x}\sin x\,dx =-\,\dfrac{1}{2}e^{-x}\cos x-\dfrac{1}{2}e^{-x}\sin x+C\)

    We first take the parts: \[\begin{array}{ll} u=e^{-x} & dv=\sin x\,dx \\ du=-e^{-x}\,dx \quad & v=-\cos x \end{array}\] Then: \[ \int e^{-x}\sin x\,dx =-e^{-x}\cos x-\int e^{-x}\cos x\,dx \] We now take the parts \[\begin{array}{ll} u=e^{-x} & dv=\cos x\,dx \\ du=-e^{-x}\,dx \quad & v=\sin x \end{array}\] Hence \[\begin{aligned} \int e^{-x}\sin x\,dx &=-e^{-x}\cos x \\ &\quad-\left(e^{-x}\sin x+\int e^{-x}\sin x\,dx\right) \\ &=-e^{-x}\cos x-e^{-x}\sin x-\int e^{-x}\sin x\,dx \end{aligned}\] We now add \(\displaystyle \int e^{-x}\sin x\,dx\) to both sides and divide by \(2\): \[\begin{aligned} 2\int e^{-x}\sin x\,dx &=-e^{-x}\cos x-e^{-x}\sin x+K \\ \int e^{-x}\sin x\,dx &=-\,\dfrac{1}{2}e^{-x}\cos x-\dfrac{1}{2}e^{-x}\sin x+C \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-\,\dfrac{1}{2}e^{-x}\cos x-\dfrac{1}{2}e^{-x}\sin x\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}e^{-x}\cos x+\dfrac{1}{2}e^{-x}\sin x +\dfrac{1}{2}e^{-x}\sin x-\dfrac{1}{2}e^{-x}\cos x \\ &=e^{-x}\sin x \end{aligned}\]

    In the solution, \(u=e^{-x}\) in both integrations by parts. It can also be done taking \(dv=e^{-x}\,dx\) in both integrations by parts.

80. \(\displaystyle \int x\sin x\cos x\,dx\)

    Use either \(\displaystyle \int \sin x\cos x\,dx=\dfrac{1}{2}\sin^2 x\) or \(\sin x\cos x=\dfrac{1}{2}\sin 2x\).

    Here are two equivalent answers: \[\begin{aligned} \int x\sin x\cos x\,dx &=\dfrac{x}{2}\sin^2 x-\dfrac{x}{4}+\dfrac{1}{8}\sin2x+C \\ &=-\,\dfrac{x}{4}\cos 2x+\dfrac{1}{8}\sin 2x+C \end{aligned}\]

    We take the parts: \[\begin{array}{ll} u=x & dv=\sin x\cos x\,dx \\ du=dx \quad & v=\dfrac{1}{2}\sin^2 x \end{array}\] Then: \[\begin{aligned} \int x\sin x\cos x\,dx &=\dfrac{x}{2}\sin^2 x-\dfrac{1}{2}\int \sin^2 x\,dx \\ &=\dfrac{x}{2}\sin^2 x-\dfrac{1}{4}\int (1-\cos 2x)\,dx \\ &=\dfrac{x}{2}\sin^2 x-\dfrac{x}{4}+\dfrac{1}{8}\sin2x+C \end{aligned}\] where we have used the the identity \(\sin^2 x=\dfrac{1-\cos 2x}{2}\).

    It is slightly easier, to start with the identity \(\sin x\cos x=\dfrac{1}{2}\sin 2x\). So: \[ \int x\sin x\cos x\,dx=\dfrac{1}{2}\int x\sin 2x\,dx \] We can now use the part: \[\begin{array}{ll} u=x & dv=\sin 2x\,dx \\ du=dx \quad & v=-\,\dfrac{1}{2}\cos 2x \end{array}\] Then: \[\begin{aligned} \int x\sin x\cos x\,dx &=\dfrac{1}{2}\left(-\dfrac{x}{2}\cos 2x+\dfrac{1}{2}\int \cos 2x\,dx\right) \\ &=-\,\dfrac{x}{4}\cos 2x+\dfrac{1}{8}\sin 2x+C \end{aligned}\]

    ---

    The answers are the same because \[\begin{aligned} \dfrac{x}{2}\sin^2 x-\dfrac{x}{4}+\dfrac{1}{8}\sin 2x &=\dfrac{x}{2}\dfrac{1-\cos 2x}{2}-\dfrac{x}{4}+\dfrac{1}{8}\sin 2x \\ &=\dfrac{x}{4}-\dfrac{x}{4}\cos 2x-\dfrac{x}{4}+\dfrac{1}{8}\sin 2x \\ &=-\,\dfrac{x}{4}\cos 2x+\dfrac{1}{8}\sin 2x \\ \end{aligned}\]

    lk 

    For the Method 1 answer, we check using the Product Rule and the square identity \(\sin^2 x=\dfrac{1-\cos 2x}{2}\). If   \(f(x)=\dfrac{x}{2}\sin^2 x-\dfrac{x}{4}+\dfrac{1}{8}\sin2x\),   then \[\begin{aligned} f'(x) &=\dfrac{1}{2}\sin^2 x+x\sin x\cos x-\dfrac{1}{4}+\dfrac{1}{4}\cos 2x \\ &=\dfrac{1}{4}(1-\cos 2x)+x\sin x\cos x-\dfrac{1}{4}+\dfrac{1}{4}\cos 2x \\ &=x\sin x\cos x \end{aligned}\]

    For the Method 2 answer, we check using the Product Rule. If   \(f(x)=-\,\dfrac{x}{4}\cos 2x+\dfrac{1}{8}\sin 2x\),   then \[\begin{aligned} f'(x) &=-\,\dfrac{1}{4}\cos 2x+\dfrac{x}{2}\sin 2x+\dfrac{1}{4}\cos 2x \\ &=\dfrac{x}{2}\left(2\sin x\cos x\right) \\ &=x\sin x\cos x \end{aligned}\]

81. \(\displaystyle \int x^3(x^2+1)^{1/2}\,dx\)

    The substitution \(u=x^2+1\) is easier than parts.

    \(\displaystyle \int x^3(x^2+1)^{1/2}\,dx =\dfrac{1}{5}(x^2+1)^{5/2}-\dfrac{1}{3}(x^2+1)^{3/2}+C\)
    If you use parts, you may get a different but equivalent answer.

    We use the substitution \(u=x^2+1\). Then \(du=2x\,dx\),   \(x\,dx=\dfrac{1}{2}\,du\) and \(x^2=u-1\). So: \[\begin{aligned} \int x^3(x^2+1)^{1/2}\,dx &=\dfrac{1}{2}\int (u-1)u^{1/2}\,du \\ &=\dfrac{1}{2}\int u^{3/2}-u^{1/2}\,du \\ &=\dfrac{1}{2}\dfrac{2u^{5/2}}{5}-\dfrac{1}{2}\dfrac{2u^{3/2}}{3}+C \\ &=\dfrac{1}{5}(x^2+1)^{5/2}-\dfrac{1}{3}(x^2+1)^{3/2}+C \\ \end{aligned}\]

    lk 

    We check using the Chain Rule. If   \(f(x)=\dfrac{1}{5}(x^2+1)^{5/2}-\dfrac{1}{3}(x^2+1)^{3/2}\),   then \[\begin{aligned} f'(x) &=x\left(x^2+1\right)^{3/2}-x\left(x^2+1\right)^{1/2} \\ &=x\left(x^2+1\right)^{1/2}\left(x^2+1-1\right) \\ &=x^3\left(x^2+1\right)^{1/2} \end{aligned}\]

---

82. Find the area of the region below \(y=x\sin\left(\dfrac{x}{2}\right)\) above the \(x\)-axis between \(x=0\) to \(x=\pi\).

    

    The area is \(\displaystyle A=\int_0^\pi x\sin\left(\dfrac{x}{2}\right)\,dx\).

    \(\displaystyle A=\int_0^\pi x\sin\left(\dfrac{x}{2}\right)\,dx=4\)

    The area is \(\displaystyle A=\int_0^\pi x\sin\left(\dfrac{x}{2}\right)\,dx\). We use the parts: \[\begin{array}{ll} u=x & dv=\sin\left(\dfrac{x}{2}\right)\,dx \\ du=dx \quad & v=-2\cos\left(\dfrac{x}{2}\right) \end{array}\] Then: \[\begin{aligned} \int x\sin\left(\dfrac{x}{2}\right)\,dx &=-2x\cos\left(\dfrac{x}{2}\right)+2\int \cos\left(\dfrac{x}{2}\right)\,dx \\ &=-2x\cos\left(\dfrac{x}{2}\right)+4\sin\left(\dfrac{x}{2}\right)+C \end{aligned}\] So the area is: \[\begin{aligned} A&=\int_0^\pi x\sin\left(\dfrac{x}{2}\right)\,dx \\ &=\left[-2x\cos\left(\dfrac{x}{2}\right) +4\sin\left(\dfrac{x}{2}\right)\right]_0^\pi \\ &=\left[-2\pi\cos\left(\dfrac{\pi}{2}\right) +4\sin\left(\dfrac{\pi}{2}\right)\right]-(0)=4 \end{aligned}\]

    lk 

    We check using the Product Rule. If   \(f(x)=-2x\cos\left(\dfrac{x}{2}\right)+4\sin\left(\dfrac{x}{2}\right)\),   then \[\begin{aligned} f'(x) &=-2\cos\left(\dfrac{x}{2}\right)+x\sin\left(\dfrac{x}{2}\right) +2\cos\left(\dfrac{x}{2}\right) \\ &=x\sin\left(\dfrac{x}{2}\right) \end{aligned}\]

PY: Everything Checked Twice